Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Lazy Lagrangians with Predictions for Online Learning

We consider the general problem of online convex optimization with time-varying additive constraints in the presence of predictions for the next cost and constraint functions. A novel primal-dual algorithm is designed by combining a Follow-The-Regularized-Leader iteration with prediction-adaptive dynamic steps. 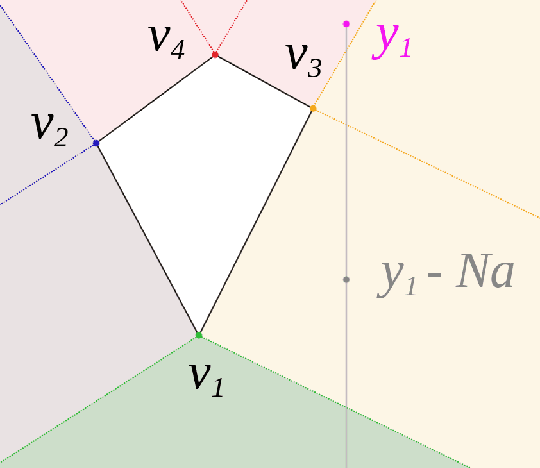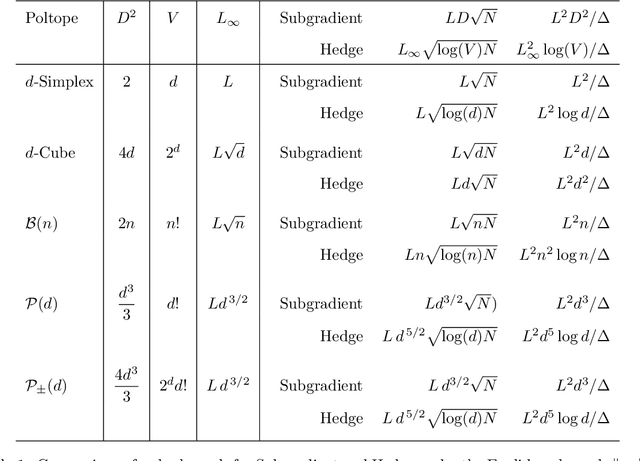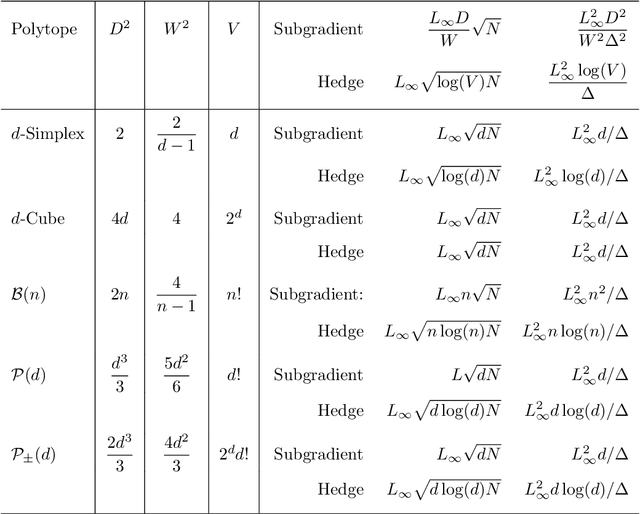The algorithm achieves $\mathcal O(T^{\frac{3-\beta}{4}})$ regret and $\mathcal O(T^{\frac{1+\beta}{2}})$ constraint violation bounds that are tunable via parameter $\beta\!\in\![1/2,1)$ and have constant factors that shrink with the predictions quality, achieving eventually $\mathcal O(1)$ regret for perfect predictions. Our work extends the FTRL framework for this constrained OCO setting and outperforms the respective state-of-the-art greedy-based solutions, without imposing conditions on the quality of predictions, the cost functions or the geometry of constraints, beyond convexity.

Universal Algorithms: Beyond the Simplex

The bulk of universal algorithms in the online convex optimisation literature are variants of the Hedge (exponential weights) algorithm on the simplex. While these algorithms extend to polytope domains by assigning weights to the vertices, this process is computationally unfeasible for many important classes of polytopes where the number $V$ of vertices depends exponentially on the dimension $d$. In this paper we show the Subgradient algorithm is universal, meaning it has $O(\sqrt N)$ regret in the antagonistic setting and $O(1)$ pseudo-regret in the i.i.d setting, with two main advantages over Hedge: (1) The update step is more efficient as the action vectors have length only $d$ rather than $V$; and (2) Subgradient gives better performance if the cost vectors satisfy Euclidean rather than sup-norm bounds. This paper extends the authors' recent results for Subgradient on the simplex. We also prove the same $O(\sqrt N)$ and $O(1)$ bounds when the domain is the unit ball. To the authors' knowledge this is the first instance of these bounds on a domain other than a polytope.

Learning The Best Expert Efficiently

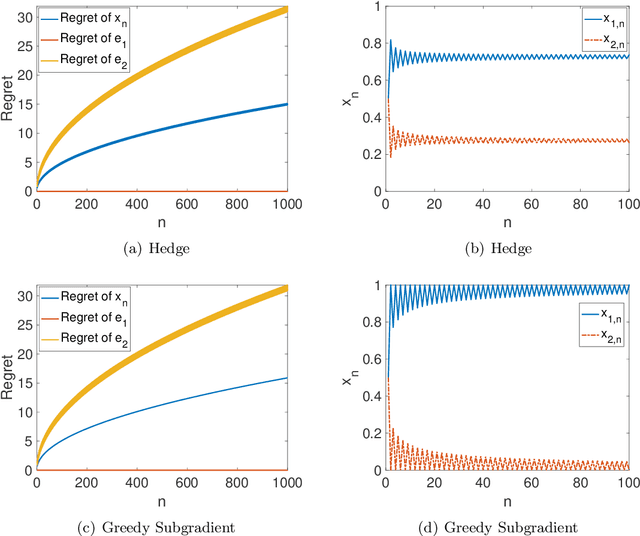
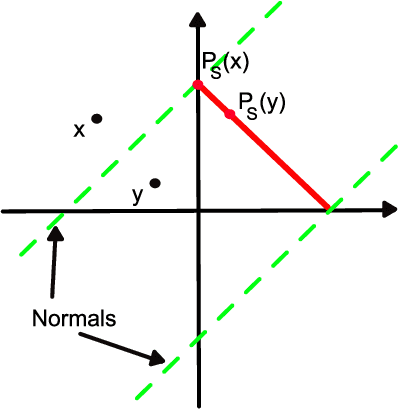
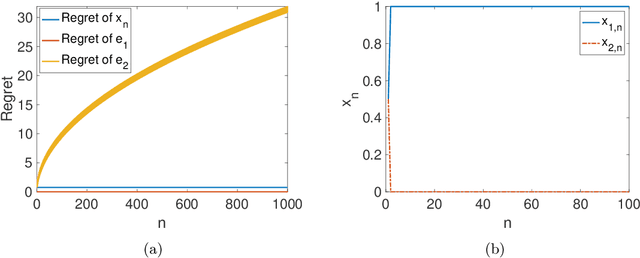
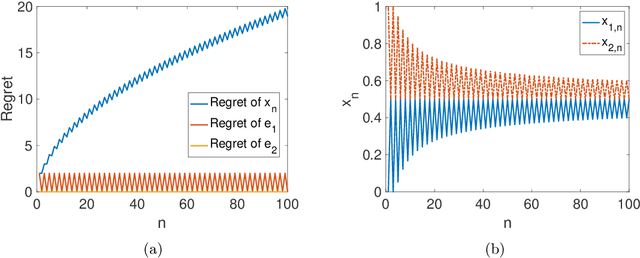
We consider online learning problems where the aim is to achieve regret which is efficient in the sense that it is the same order as the lowest regret amongst K experts. This is a substantially stronger requirement that achieving $O(\sqrt{n})$ or $O(\log n)$ regret with respect to the best expert and standard algorithms are insufficient, even in easy cases where the regrets of the available actions are very different from one another. We show that a particular lazy form of the online subgradient algorithm can be used to achieve minimal regret in a number of "easy" regimes while retaining an $O(\sqrt{n})$ worst-case regret guarantee. We also show that for certain classes of problem minimal regret strategies exist for some of the remaining "hard" regimes.

Optimality of the Subgradient Algorithm in the Stochastic Setting

Recently Jaouad Mourtada and St\' ephane Ga\"iffas showed the anytime hedge algorithm has pseudo-regret $O(\log (d) / \Delta)$ if the cost vectors are generated by an i.i.d sequence in the cube $[0,1]^d$. Here $d$ is the dimension and $\Delta$ the suboptimality gap. This is remarkable because the Hedge algorithm was designed for the antagonistic setting. We prove a similar result for the anytime subgradient algorithm on the simplex. Given i.i.d cost vectors in the unit ball our pseudo-regret bound is $O(1/\Delta)$ and does not depend on the dimension of the problem.