Learning The Best Expert Efficiently
Paper and Code
Nov 11, 2019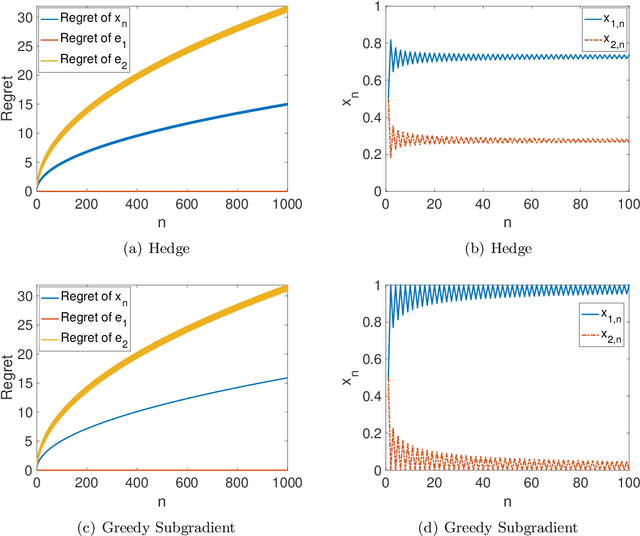
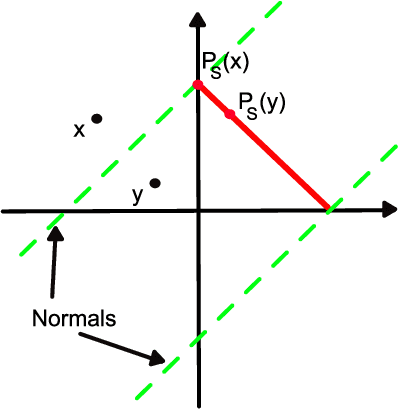
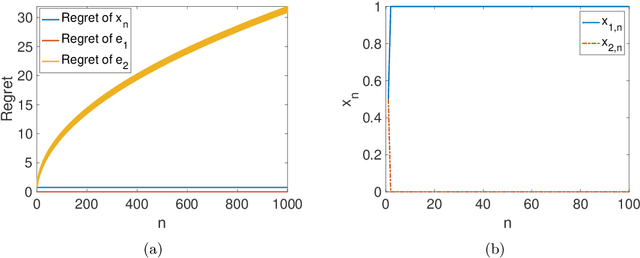
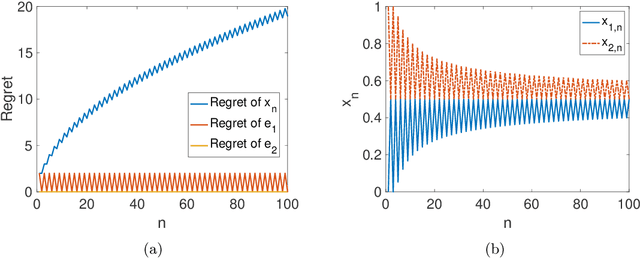
We consider online learning problems where the aim is to achieve regret which is efficient in the sense that it is the same order as the lowest regret amongst K experts. This is a substantially stronger requirement that achieving $O(\sqrt{n})$ or $O(\log n)$ regret with respect to the best expert and standard algorithms are insufficient, even in easy cases where the regrets of the available actions are very different from one another. We show that a particular lazy form of the online subgradient algorithm can be used to achieve minimal regret in a number of "easy" regimes while retaining an $O(\sqrt{n})$ worst-case regret guarantee. We also show that for certain classes of problem minimal regret strategies exist for some of the remaining "hard" regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge