Universal Algorithms: Beyond the Simplex

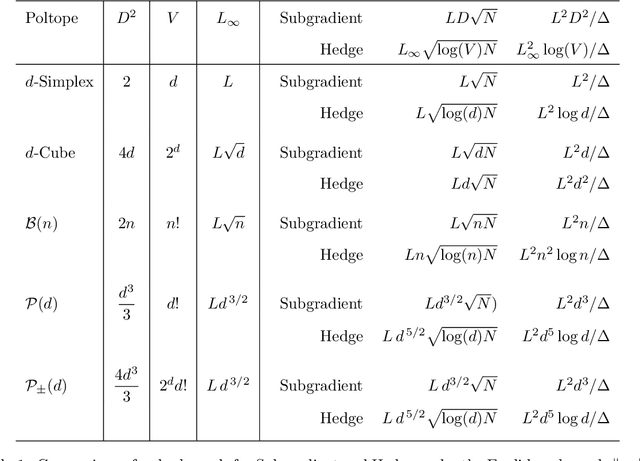
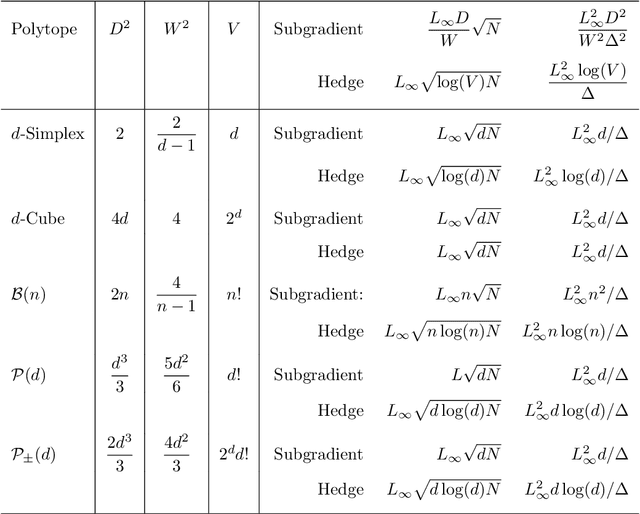
The bulk of universal algorithms in the online convex optimisation literature are variants of the Hedge (exponential weights) algorithm on the simplex. While these algorithms extend to polytope domains by assigning weights to the vertices, this process is computationally unfeasible for many important classes of polytopes where the number $V$ of vertices depends exponentially on the dimension $d$. In this paper we show the Subgradient algorithm is universal, meaning it has $O(\sqrt N)$ regret in the antagonistic setting and $O(1)$ pseudo-regret in the i.i.d setting, with two main advantages over Hedge: (1) The update step is more efficient as the action vectors have length only $d$ rather than $V$; and (2) Subgradient gives better performance if the cost vectors satisfy Euclidean rather than sup-norm bounds. This paper extends the authors' recent results for Subgradient on the simplex. We also prove the same $O(\sqrt N)$ and $O(1)$ bounds when the domain is the unit ball. To the authors' knowledge this is the first instance of these bounds on a domain other than a polytope.