GOAL: A Generalist Combinatorial Optimization Agent Learner

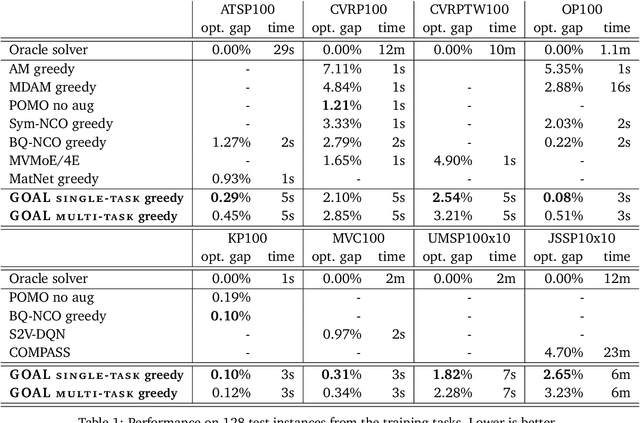
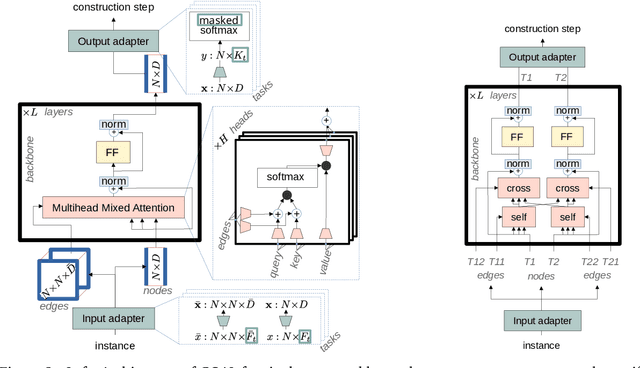
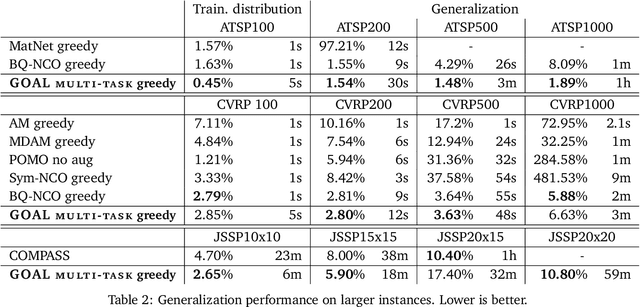
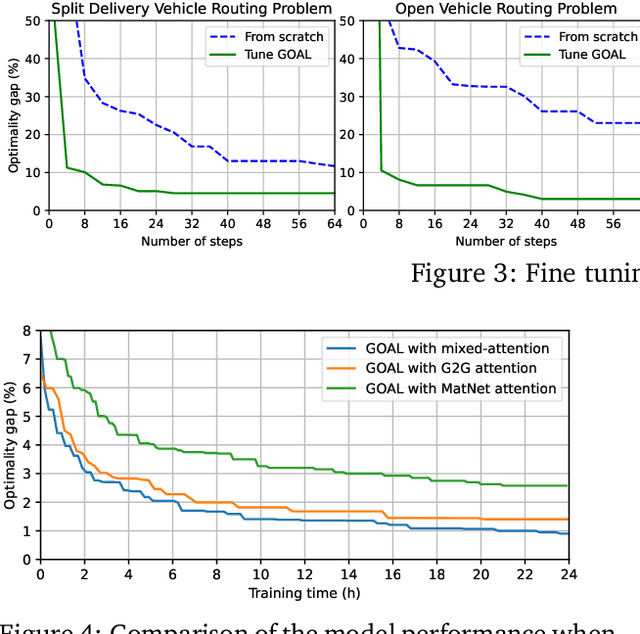
Machine Learning-based heuristics have recently shown impressive performance in solving a variety of hard combinatorial optimization problems (COPs). However they generally rely on a separate neural model, specialized and trained for each single problem. Any variation of a problem requires adjustment of its model and re-training from scratch. In this paper, we propose GOAL (for Generalist combinatorial Optimization Agent Learning), a generalist model capable of efficiently solving multiple COPs and which can be fine-tuned to solve new COPs. GOAL consists of a single backbone plus light-weight problem-specific adapters, mostly for input and output processing. The backbone is based on a new form of mixed-attention blocks which allows to handle problems defined on graphs with arbitrary combinations of node, edge and instance-level features. Additionally, problems which involve heterogeneous nodes or edges, such as in multi-partite graphs, are handled through a novel multi-type transformer architecture, where the attention blocks are duplicated to attend only the relevant combination of types while relying on the same shared parameters. We train GOAL on a set of routing, scheduling and classic graph problems and show that it is only slightly inferior to the specialized baselines while being the first multi-task model that solves a variety of COPs. Finally, we showcase the strong transfer learning capacity of GOAL by fine-tuning or learning the adapters for new problems, with only few shots and little data.

BQ-NCO: Bisimulation Quotienting for Generalizable Neural Combinatorial Optimization

Despite the success of Neural Combinatorial Optimization methods for end-to-end heuristic learning, out-of-distribution generalization remains a challenge. In this paper, we present a novel formulation of combinatorial optimization (CO) problems as Markov Decision Processes (MDPs) that effectively leverages symmetries of the CO problems to improve out-of-distribution robustness. Starting from the standard MDP formulation of constructive heuristics, we introduce a generic transformation based on bisimulation quotienting (BQ) in MDPs. This transformation allows to reduce the state space by accounting for the intrinsic symmetries of the CO problem and facilitates the MDP solving. We illustrate our approach on the Traveling Salesman, Capacitated Vehicle Routing and Knapsack Problems. We present a BQ reformulation of these problems and introduce a simple attention-based policy network that we train by imitation of (near) optimal solutions for small instances from a single distribution. We obtain new state-of-the-art generalization results for instances with up to 1000 nodes from synthetic and realistic benchmarks that vary both in size and node distributions.

On the Generalization of Neural Combinatorial Optimization Heuristics

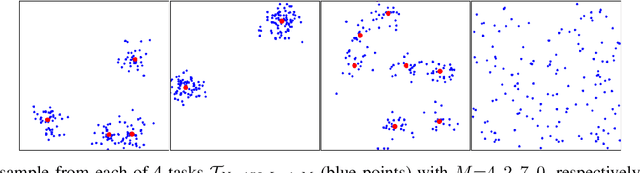
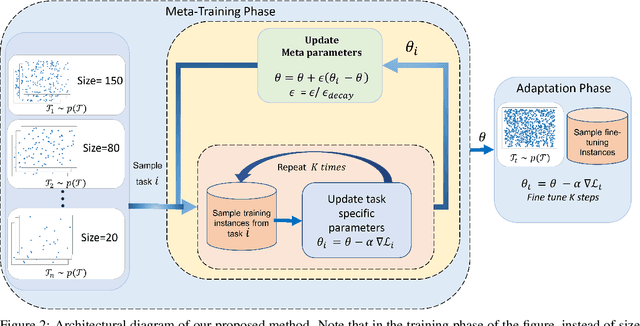
Neural Combinatorial Optimization approaches have recently leveraged the expressiveness and flexibility of deep neural networks to learn efficient heuristics for hard Combinatorial Optimization (CO) problems. However, most of the current methods lack generalization: for a given CO problem, heuristics which are trained on instances with certain characteristics underperform when tested on instances with different characteristics. While some previous works have focused on varying the training instances properties, we postulate that a one-size-fit-all model is out of reach. Instead, we formalize solving a CO problem over a given instance distribution as a separate learning task and investigate meta-learning techniques to learn a model on a variety of tasks, in order to optimize its capacity to adapt to new tasks. Through extensive experiments, on two CO problems, using both synthetic and realistic instances, we show that our proposed meta-learning approach significantly improves the generalization of two state-of-the-art models.

Structured Time Series Prediction without Structural Prior

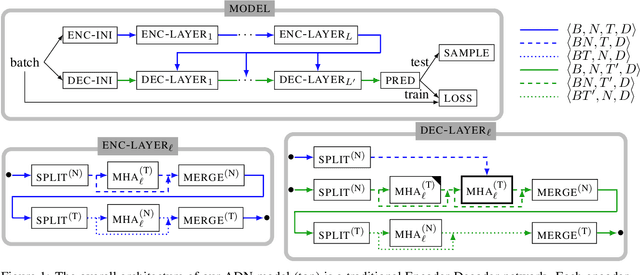
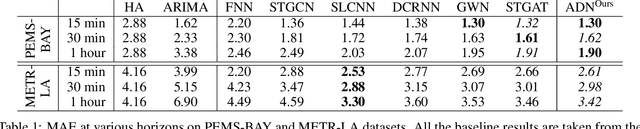
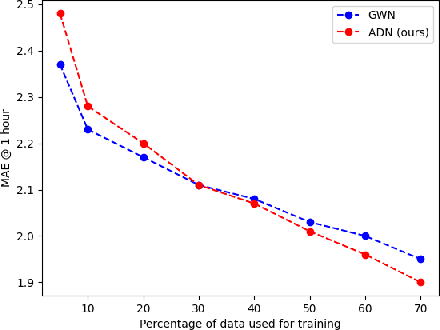
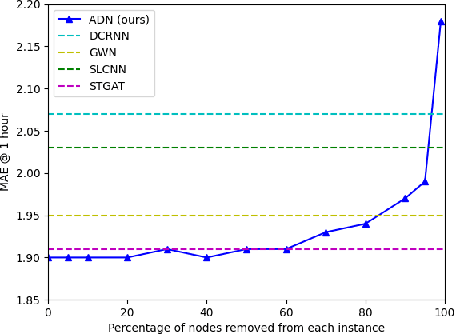
Time series prediction is a widespread and well studied problem with applications in many domains (medical, geoscience, network analysis, finance, econometry etc.). In the case of multivariate time series, the key to good performances is to properly capture the dependencies between the variates. Often, these variates are structured, i.e. they are localised in an abstract space, usually representing an aspect of the physical world, and prediction amounts to a form of diffusion of the information across that space over time. Several neural network models of diffusion have been proposed in the literature. However, most of the existing proposals rely on some a priori knowledge on the structure of the space, usually in the form of a graph weighing the pairwise diffusion capacity of its points. We argue that this piece of information can often be dispensed with, since data already contains the diffusion capacity information, and in a more reliable form than that obtained from the usually largely hand-crafted graphs. We propose instead a fully data-driven model which does not rely on such a graph, nor any other prior structural information. We conduct a first set of experiments to measure the impact on performance of a structural prior, as used in baseline models, and show that, except at very low data levels, it remains negligible, and beyond a threshold, it may even become detrimental. We then investigate, through a second set of experiments, the capacity of our model in two respects: treatment of missing data and domain adaptation.