Generalised envelope spectrum-based signal-to-noise objectives: Formulation, optimisation and application for gear fault detection under time-varying speed conditions

In vibration-based condition monitoring, optimal filter design improves fault detection by enhancing weak fault signatures within vibration signals. This process involves optimising a derived objective function from a defined objective. The objectives are often based on proxy health indicators to determine the filter's parameters. However, these indicators can be compromised by irrelevant extraneous signal components and fluctuating operational conditions, affecting the filter's efficacy. Fault detection primarily uses the fault component's prominence in the squared envelope spectrum, quantified by a squared envelope spectrum-based signal-to-noise ratio. New optimal filter objective functions are derived from the proposed generalised envelope spectrum-based signal-to-noise objective for machines operating under variable speed conditions. Instead of optimising proxy health indicators, the optimal filter coefficients of the formulation directly maximise the squared envelope spectrum-based signal-to-noise ratio over targeted frequency bands using standard gradient-based optimisers. Four derived objective functions from the proposed objective effectively outperform five prominent methods in tests on three experimental datasets.

A spectral regularisation framework for latent variable models designed for single channel applications

Latent variable models (LVMs) are commonly used to capture the underlying dependencies, patterns, and hidden structure in observed data. Source duplication is a by-product of the data hankelisation pre-processing step common to single channel LVM applications, which hinders practical LVM utilisation. In this article, a Python package titled spectrally-regularised-LVMs is presented. The proposed package addresses the source duplication issue via the addition of a novel spectral regularisation term. This package provides a framework for spectral regularisation in single channel LVM applications, thereby making it easier to investigate and utilise LVMs with spectral regularisation. This is achieved via the use of symbolic or explicit representations of potential LVM objective functions which are incorporated into a framework that uses spectral regularisation during the LVM parameter estimation process. The objective of this package is to provide a consistent linear LVM optimisation framework which incorporates spectral regularisation and caters to single channel time-series applications.

Latent Space Perspicacity and Interpretation Enhancement (LS-PIE) Framework

Linear latent variable models such as principal component analysis (PCA), independent component analysis (ICA), canonical correlation analysis (CCA), and factor analysis (FA) identify latent directions (or loadings) either ordered or unordered. The data is then projected onto the latent directions to obtain their projected representations (or scores). For example, PCA solvers usually rank the principal directions by explaining the most to least variance, while ICA solvers usually return independent directions unordered and often with single sources spread across multiple directions as multiple sub-sources, which is of severe detriment to their usability and interpretability. This paper proposes a general framework to enhance latent space representations for improving the interpretability of linear latent spaces. Although the concepts in this paper are language agnostic, the framework is written in Python. This framework automates the clustering and ranking of latent vectors to enhance the latent information per latent vector, as well as, the interpretation of latent vectors. Several innovative enhancements are incorporated including latent ranking (LR), latent scaling (LS), latent clustering (LC), and latent condensing (LCON). For a specified linear latent variable model, LR ranks latent directions according to a specified metric, LS scales latent directions according to a specified metric, LC automatically clusters latent directions into a specified number of clusters, while, LCON automatically determines an appropriate number of clusters into which to condense the latent directions for a given metric. Additional functionality of the framework includes single-channel and multi-channel data sources, data preprocessing strategies such as Hankelisation to seamlessly expand the applicability of linear latent variable models (LLVMs) to a wider variety of data. The effectiveness of LR, LS, and LCON are showcased on two crafted foundational problems with two applied latent variable models, namely, PCA and ICA.

GOALS: Gradient-Only Approximations for Line Searches Towards Robust and Consistent Training of Deep Neural Networks

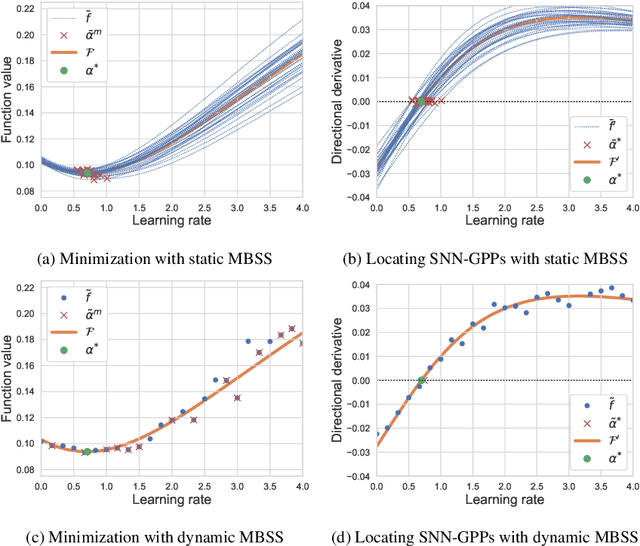
Mini-batch sub-sampling (MBSS) is favored in deep neural network training to reduce the computational cost. Still, it introduces an inherent sampling error, making the selection of appropriate learning rates challenging. The sampling errors can manifest either as a bias or variances in a line search. Dynamic MBSS re-samples a mini-batch at every function evaluation. Hence, dynamic MBSS results in point-wise discontinuous loss functions with smaller bias but larger variance than static sampled loss functions. However, dynamic MBSS has the advantage of having larger data throughput during training but requires the complexity regarding discontinuities to be resolved. This study extends the gradient-only surrogate (GOS), a line search method using quadratic approximation models built with only directional derivative information, for dynamic MBSS loss functions. We propose a gradient-only approximation line search (GOALS) with strong convergence characteristics with defined optimality criterion. We investigate GOALS's performance by applying it on various optimizers that include SGD, RMSprop and Adam on ResNet-18 and EfficientNetB0. We also compare GOALS's against the other existing learning rate methods. We quantify both the best performing and most robust algorithms. For the latter, we introduce a relative robust criterion that allows us to quantify the difference between an algorithm and the best performing algorithm for a given problem. The results show that training a model with the recommended learning rate for a class of search directions helps to reduce the model errors in multimodal cases.

Resolving learning rates adaptively by locating Stochastic Non-Negative Associated Gradient Projection Points using line searches

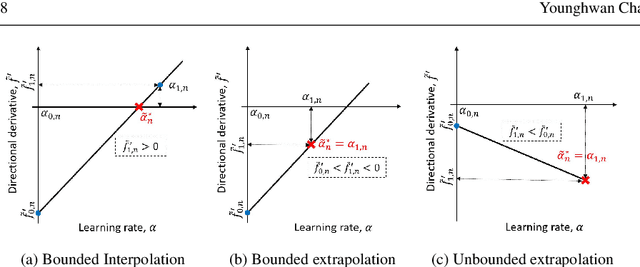
Learning rates in stochastic neural network training are currently determined a priori to training, using expensive manual or automated iterative tuning. This study proposes gradient-only line searches to resolve the learning rate for neural network training algorithms. Stochastic sub-sampling during training decreases computational cost and allows the optimization algorithms to progress over local minima. However, it also results in discontinuous cost functions. Minimization line searches are not effective in this context, as they use a vanishing derivative (first order optimality condition), which often do not exist in a discontinuous cost function and therefore converge to discontinuities as opposed to minima from the data trends. Instead, we base candidate solutions along a search direction purely on gradient information, in particular by a directional derivative sign change from negative to positive (a Non-negative Associative Gradient Projection Point (NN- GPP)). Only considering a sign change from negative to positive always indicates a minimum, thus NN-GPPs contain second order information. Conversely, a vanishing gradient is purely a first order condition, which may indicate a minimum, maximum or saddle point. This insight allows the learning rate of an algorithm to be reliably resolved as the step size along a search direction, increasing convergence performance and eliminating an otherwise expensive hyperparameter.

Empirical study towards understanding line search approximations for training neural networks

Choosing appropriate step sizes is critical for reducing the computational cost of training large-scale neural network models. Mini-batch sub-sampling (MBSS) is often employed for computational tractability. However, MBSS introduces a sampling error, that can manifest as a bias or variance in a line search. This is because MBSS can be performed statically, where the mini-batch is updated only when the search direction changes, or dynamically, where the mini-batch is updated every-time the function is evaluated. Static MBSS results in a smooth loss function along a search direction, reflecting low variance but large bias in the estimated "true" (or full batch) minimum. Conversely, dynamic MBSS results in a point-wise discontinuous function, with computable gradients using backpropagation, along a search direction, reflecting high variance but lower bias in the estimated "true" (or full batch) minimum. In this study, quadratic line search approximations are considered to study the quality of function and derivative information to construct approximations for dynamic MBSS loss functions. An empirical study is conducted where function and derivative information are enforced in various ways for the quadratic approximations. The results for various neural network problems show that being selective on what information is enforced helps to reduce the variance of predicted step sizes.