GOALS: Gradient-Only Approximations for Line Searches Towards Robust and Consistent Training of Deep Neural Networks

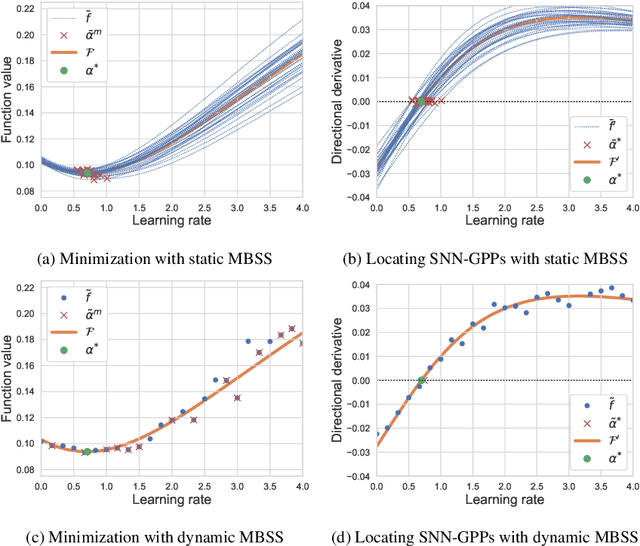
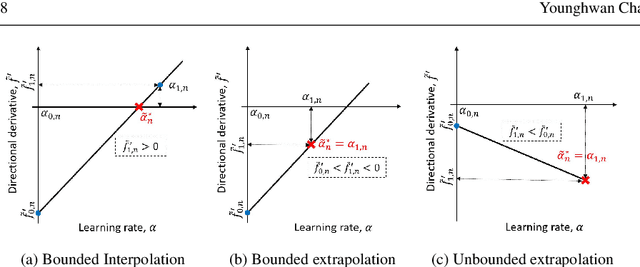
Mini-batch sub-sampling (MBSS) is favored in deep neural network training to reduce the computational cost. Still, it introduces an inherent sampling error, making the selection of appropriate learning rates challenging. The sampling errors can manifest either as a bias or variances in a line search. Dynamic MBSS re-samples a mini-batch at every function evaluation. Hence, dynamic MBSS results in point-wise discontinuous loss functions with smaller bias but larger variance than static sampled loss functions. However, dynamic MBSS has the advantage of having larger data throughput during training but requires the complexity regarding discontinuities to be resolved. This study extends the gradient-only surrogate (GOS), a line search method using quadratic approximation models built with only directional derivative information, for dynamic MBSS loss functions. We propose a gradient-only approximation line search (GOALS) with strong convergence characteristics with defined optimality criterion. We investigate GOALS's performance by applying it on various optimizers that include SGD, RMSprop and Adam on ResNet-18 and EfficientNetB0. We also compare GOALS's against the other existing learning rate methods. We quantify both the best performing and most robust algorithms. For the latter, we introduce a relative robust criterion that allows us to quantify the difference between an algorithm and the best performing algorithm for a given problem. The results show that training a model with the recommended learning rate for a class of search directions helps to reduce the model errors in multimodal cases.

Empirical study towards understanding line search approximations for training neural networks

Choosing appropriate step sizes is critical for reducing the computational cost of training large-scale neural network models. Mini-batch sub-sampling (MBSS) is often employed for computational tractability. However, MBSS introduces a sampling error, that can manifest as a bias or variance in a line search. This is because MBSS can be performed statically, where the mini-batch is updated only when the search direction changes, or dynamically, where the mini-batch is updated every-time the function is evaluated. Static MBSS results in a smooth loss function along a search direction, reflecting low variance but large bias in the estimated "true" (or full batch) minimum. Conversely, dynamic MBSS results in a point-wise discontinuous function, with computable gradients using backpropagation, along a search direction, reflecting high variance but lower bias in the estimated "true" (or full batch) minimum. In this study, quadratic line search approximations are considered to study the quality of function and derivative information to construct approximations for dynamic MBSS loss functions. An empirical study is conducted where function and derivative information are enforced in various ways for the quadratic approximations. The results for various neural network problems show that being selective on what information is enforced helps to reduce the variance of predicted step sizes.