Resolving learning rates adaptively by locating Stochastic Non-Negative Associated Gradient Projection Points using line searches

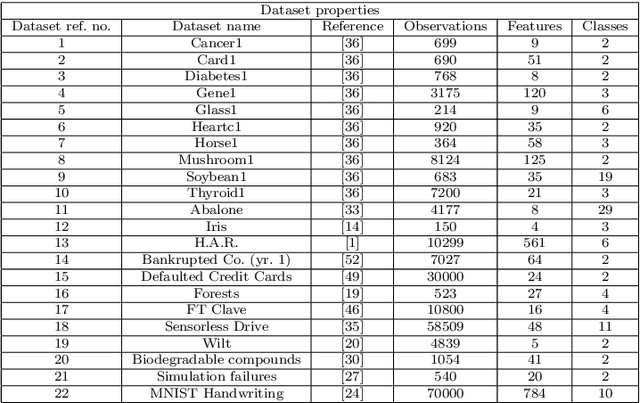
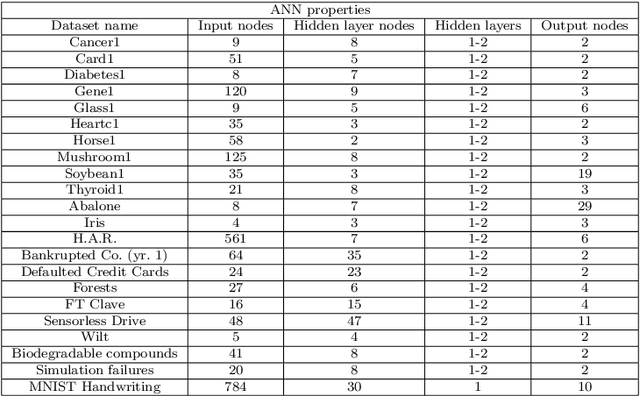
Learning rates in stochastic neural network training are currently determined a priori to training, using expensive manual or automated iterative tuning. This study proposes gradient-only line searches to resolve the learning rate for neural network training algorithms. Stochastic sub-sampling during training decreases computational cost and allows the optimization algorithms to progress over local minima. However, it also results in discontinuous cost functions. Minimization line searches are not effective in this context, as they use a vanishing derivative (first order optimality condition), which often do not exist in a discontinuous cost function and therefore converge to discontinuities as opposed to minima from the data trends. Instead, we base candidate solutions along a search direction purely on gradient information, in particular by a directional derivative sign change from negative to positive (a Non-negative Associative Gradient Projection Point (NN- GPP)). Only considering a sign change from negative to positive always indicates a minimum, thus NN-GPPs contain second order information. Conversely, a vanishing gradient is purely a first order condition, which may indicate a minimum, maximum or saddle point. This insight allows the learning rate of an algorithm to be reliably resolved as the step size along a search direction, increasing convergence performance and eliminating an otherwise expensive hyperparameter.