Stable Training of Normalizing Flows for High-dimensional Variational Inference

Variational inference with normalizing flows (NFs) is an increasingly popular alternative to MCMC methods. In particular, NFs based on coupling layers (Real NVPs) are frequently used due to their good empirical performance. In theory, increasing the depth of normalizing flows should lead to more accurate posterior approximations. However, in practice, training deep normalizing flows for approximating high-dimensional posterior distributions is often infeasible due to the high variance of the stochastic gradients. In this work, we show that previous methods for stabilizing the variance of stochastic gradient descent can be insufficient to achieve stable training of Real NVPs. As the source of the problem, we identify that, during training, samples often exhibit unusual high values. As a remedy, we propose a combination of two methods: (1) soft-thresholding of the scale in Real NVPs, and (2) a bijective soft log transformation of the samples. We evaluate these and other previously proposed modification on several challenging target distributions, including a high-dimensional horseshoe logistic regression model. Our experiments show that with our modifications, stable training of Real NVPs for posteriors with several thousand dimensions is possible, allowing for more accurate marginal likelihood estimation via importance sampling. Moreover, we evaluate several common training techniques and architecture choices and provide practical advise for training NFs for high-dimensional variational inference.

YOLOv7 for Mosquito Breeding Grounds Detection and Tracking

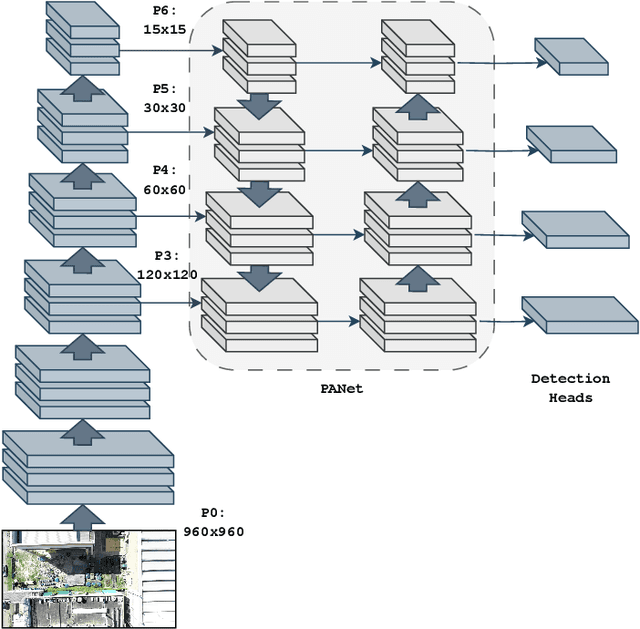
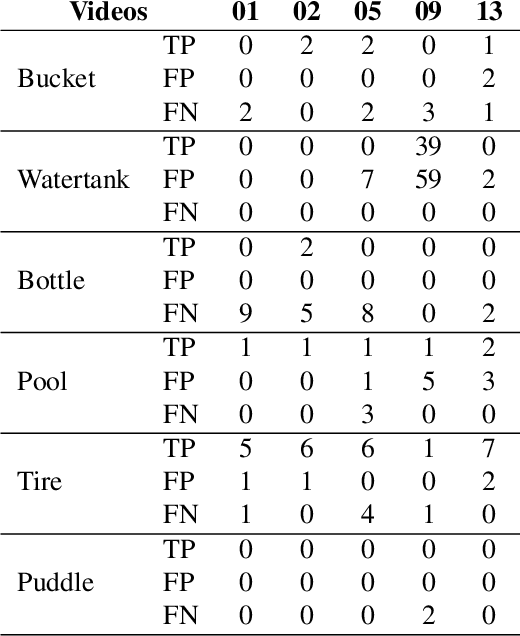
With the looming threat of climate change, neglected tropical diseases such as dengue, zika, and chikungunya have the potential to become an even greater global concern. Remote sensing technologies can aid in controlling the spread of Aedes Aegypti, the transmission vector of such diseases, by automating the detection and mapping of mosquito breeding sites, such that local entities can properly intervene. In this work, we leverage YOLOv7, a state-of-the-art and computationally efficient detection approach, to localize and track mosquito foci in videos captured by unmanned aerial vehicles. We experiment on a dataset released to the public as part of the ICIP 2023 grand challenge entitled Automatic Detection of Mosquito Breeding Grounds. We show that YOLOv7 can be directly applied to detect larger foci categories such as pools, tires, and water tanks and that a cheap and straightforward aggregation of frame-by-frame detection can incorporate time consistency into the tracking process.

Adaptive Covariate Acquisition for Minimizing Total Cost of Classification

In some applications, acquiring covariates comes at a cost which is not negligible. For example in the medical domain, in order to classify whether a patient has diabetes or not, measuring glucose tolerance can be expensive. Assuming that the cost of each covariate, and the cost of misclassification can be specified by the user, our goal is to minimize the (expected) total cost of classification, i.e. the cost of misclassification plus the cost of the acquired covariates. We formalize this optimization goal using the (conditional) Bayes risk and describe the optimal solution using a recursive procedure. Since the procedure is computationally infeasible, we consequently introduce two assumptions: (1) the optimal classifier can be represented by a generalized additive model, (2) the optimal sets of covariates are limited to a sequence of sets of increasing size. We show that under these two assumptions, a computationally efficient solution exists. Furthermore, on several medical datasets, we show that the proposed method achieves in most situations the lowest total costs when compared to various previous methods. Finally, we weaken the requirement on the user to specify all misclassification costs by allowing the user to specify the minimally acceptable recall (target recall). Our experiments confirm that the proposed method achieves the target recall while minimizing the false discovery rate and the covariate acquisition costs better than previous methods.

Convex Covariate Clustering for Classification

Clustering, like covariate selection for classification, is an important step to understand and interpret the data. However, clustering of covariates is often performed independently of the classification step, which can lead to undesirable clustering results. Therefore, we propose a method that can cluster covariates while taking into account class label information of samples. We formulate the problem as a convex optimization problem which uses both, a-priori similarity information between covariates, and information from class-labeled samples. Like convex clustering [Chi and Lange, 2015], the proposed method offers a unique global minima making it insensitive to initialization. In order to solve the convex problem, we propose a specialized alternating direction method of multipliers (ADMM), which scales up to several thousands of variables. Furthermore, in order to circumvent computationally expensive cross-validation, we propose a model selection criterion based on approximate marginal likelihood estimation. Experiments on synthetic and real data confirm the usefulness of the proposed clustering method and the selection criterion.

Robust Bayesian Model Selection for Variable Clustering with the Gaussian Graphical Model

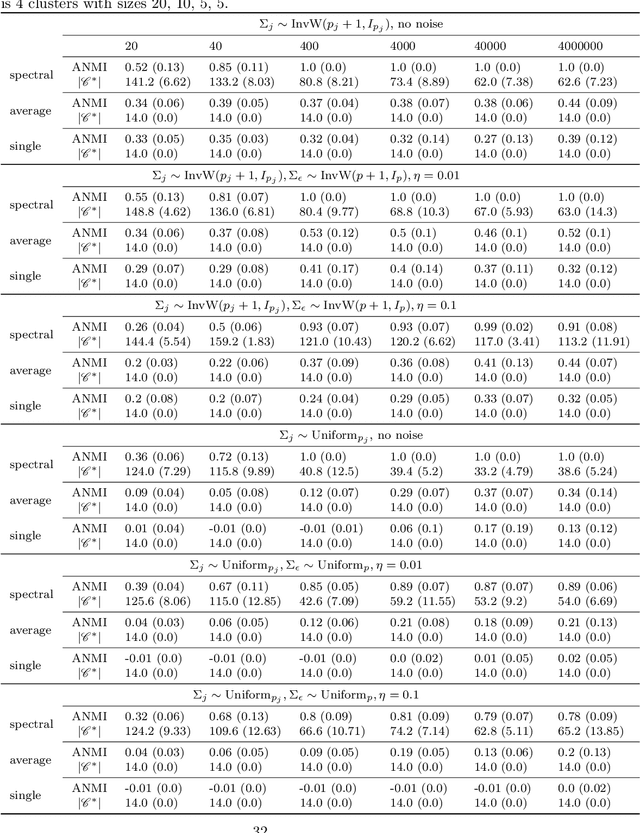
Variable clustering is important for explanatory analysis. However, only few dedicated methods for variable clustering with the Gaussian graphical model have been proposed. Even more severe, small insignificant partial correlations due to noise can dramatically change the clustering result when evaluating for example with the Bayesian Information Criteria (BIC). In this work, we try to address this issue by proposing a Bayesian model that accounts for negligible small, but not necessarily zero, partial correlations. Based on our model, we propose to evaluate a variable clustering result using the marginal likelihood. To address the intractable calculation of the marginal likelihood, we propose two solutions: one based on a variational approximation, and another based on MCMC. Experiments on simulated data shows that the proposed method is similarly accurate as BIC in the no noise setting, but considerably more accurate when there are noisy partial correlations. Furthermore, on real data the proposed method provides clustering results that are intuitively sensible, which is not always the case when using BIC or its extensions.

Lower Bound Bayesian Networks - An Efficient Inference of Lower Bounds on Probability Distributions in Bayesian Networks

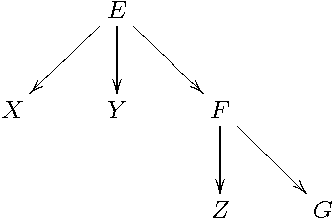
We present a new method to propagate lower bounds on conditional probability distributions in conventional Bayesian networks. Our method guarantees to provide outer approximations of the exact lower bounds. A key advantage is that we can use any available algorithms and tools for Bayesian networks in order to represent and infer lower bounds. This new method yields results that are provable exact for trees with binary variables, and results which are competitive to existing approximations in credal networks for all other network structures. Our method is not limited to a specific kind of network structure. Basically, it is also not restricted to a specific kind of inference, but we restrict our analysis to prognostic inference in this article. The computational complexity is superior to that of other existing approaches.