Boosting Few-Pixel Robustness Verification via Covering Verification Designs

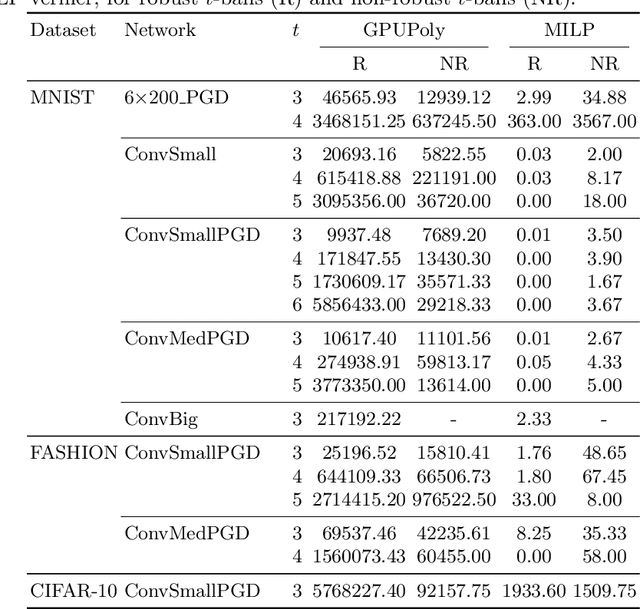
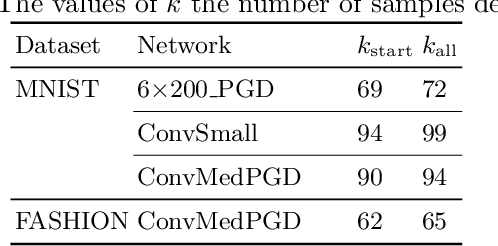
Proving local robustness is crucial to increase the reliability of neural networks. While many verifiers prove robustness in $L_\infty$ $\epsilon$-balls, very little work deals with robustness verification in $L_0$ $\epsilon$-balls, capturing robustness to few pixel attacks. This verification introduces a combinatorial challenge, because the space of pixels to perturb is discrete and of exponential size. A previous work relies on covering designs to identify sets for defining $L_\infty$ neighborhoods, which if proven robust imply that the $L_0$ $\epsilon$-ball is robust. However, the number of neighborhoods to verify remains very high, leading to a high analysis time. We propose covering verification designs, a combinatorial design that tailors effective but analysis-incompatible coverings to $L_0$ robustness verification. The challenge is that computing a covering verification design introduces a high time and memory overhead, which is intensified in our setting, where multiple candidate coverings are required to identify how to reduce the overall analysis time. We introduce CoVerD, an $L_0$ robustness verifier that selects between different candidate coverings without constructing them, but by predicting their block size distribution. This prediction relies on a theorem providing closed-form expressions for the mean and variance of this distribution. CoVerD constructs the chosen covering verification design on-the-fly, while keeping the memory consumption minimal and enabling to parallelize the analysis. The experimental results show that CoVerD reduces the verification time on average by up to 5.1x compared to prior work and that it scales to larger $L_0$ $\epsilon$-balls.

Verification of Neural Networks' Global Robustness

Neural networks are successful in various applications but are also susceptible to adversarial attacks. To show the safety of network classifiers, many verifiers have been introduced to reason about the local robustness of a given input to a given perturbation. While successful, local robustness cannot generalize to unseen inputs. Several works analyze global robustness properties, however, neither can provide a precise guarantee about the cases where a network classifier does not change its classification. In this work, we propose a new global robustness property for classifiers aiming at finding the minimal globally robust bound, which naturally extends the popular local robustness property for classifiers. We introduce VHAGaR, an anytime verifier for computing this bound. VHAGaR relies on three main ideas: encoding the problem as a mixed-integer programming and pruning the search space by identifying dependencies stemming from the perturbation or the network's computation and generalizing adversarial attacks to unknown inputs. We evaluate VHAGaR on several datasets and classifiers and show that, given a three hour timeout, the average gap between the lower and upper bound on the minimal globally robust bound computed by VHAGaR is 1.9, while the gap of an existing global robustness verifier is 154.7. Moreover, VHAGaR is 130.6x faster than this verifier. Our results further indicate that leveraging dependencies and adversarial attacks makes VHAGaR 78.6x faster.

Verification of Neural Networks Local Differential Classification Privacy

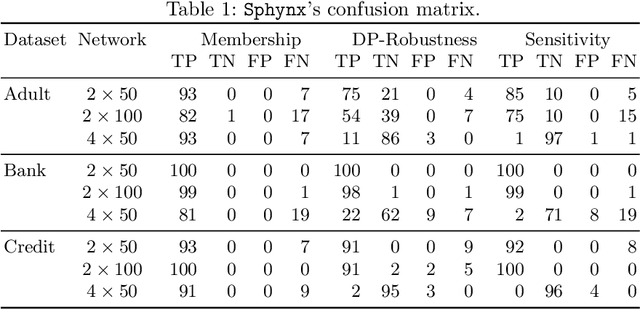
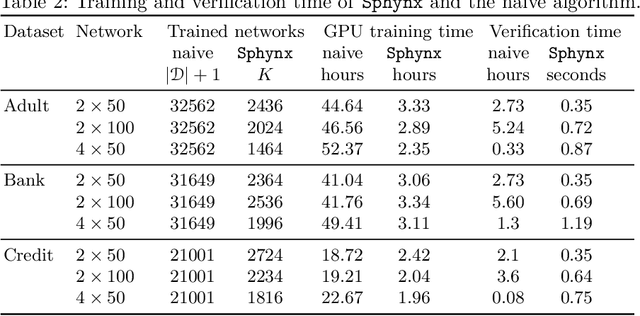
Neural networks are susceptible to privacy attacks. To date, no verifier can reason about the privacy of individuals participating in the training set. We propose a new privacy property, called local differential classification privacy (LDCP), extending local robustness to a differential privacy setting suitable for black-box classifiers. Given a neighborhood of inputs, a classifier is LDCP if it classifies all inputs the same regardless of whether it is trained with the full dataset or whether any single entry is omitted. A naive algorithm is highly impractical because it involves training a very large number of networks and verifying local robustness of the given neighborhood separately for every network. We propose Sphynx, an algorithm that computes an abstraction of all networks, with a high probability, from a small set of networks, and verifies LDCP directly on the abstract network. The challenge is twofold: network parameters do not adhere to a known distribution probability, making it difficult to predict an abstraction, and predicting too large abstraction harms the verification. Our key idea is to transform the parameters into a distribution given by KDE, allowing to keep the over-approximation error small. To verify LDCP, we extend a MILP verifier to analyze an abstract network. Experimental results show that by training only 7% of the networks, Sphynx predicts an abstract network obtaining 93% verification accuracy and reducing the analysis time by $1.7\cdot10^4$x.

Boosting Robustness Verification of Semantic Feature Neighborhoods

Deep neural networks have been shown to be vulnerable to adversarial attacks that perturb inputs based on semantic features. Existing robustness analyzers can reason about semantic feature neighborhoods to increase the networks' reliability. However, despite the significant progress in these techniques, they still struggle to scale to deep networks and large neighborhoods. In this work, we introduce VeeP, an active learning approach that splits the verification process into a series of smaller verification steps, each is submitted to an existing robustness analyzer. The key idea is to build on prior steps to predict the next optimal step. The optimal step is predicted by estimating the certification velocity and sensitivity via parametric regression. We evaluate VeeP on MNIST, Fashion-MNIST, CIFAR-10 and ImageNet and show that it can analyze neighborhoods of various features: brightness, contrast, hue, saturation, and lightness. We show that, on average, given a 90 minute timeout, VeeP verifies 96% of the maximally certifiable neighborhoods within 29 minutes, while existing splitting approaches verify, on average, 73% of the maximally certifiable neighborhoods within 58 minutes.

Learning Disjunctions of Predicates

Let $F$ be a set of boolean functions. We present an algorithm for learning $F_\vee := \{\vee_{f\in S} f \mid S \subseteq F\}$ from membership queries. Our algorithm asks at most $|F| \cdot OPT(F_\vee)$ membership queries where $OPT(F_\vee)$ is the minimum worst case number of membership queries for learning $F_\vee$. When $F$ is a set of halfspaces over a constant dimension space or a set of variable inequalities, our algorithm runs in polynomial time. The problem we address has practical importance in the field of program synthesis, where the goal is to synthesize a program that meets some requirements. Program synthesis has become popular especially in settings aiming to help end users. In such settings, the requirements are not provided upfront and the synthesizer can only learn them by posing membership queries to the end user. Our work enables such synthesizers to learn the exact requirements while bounding the number of membership queries.