Verification of Neural Networks Local Differential Classification Privacy
Paper and Code
Oct 31, 2023
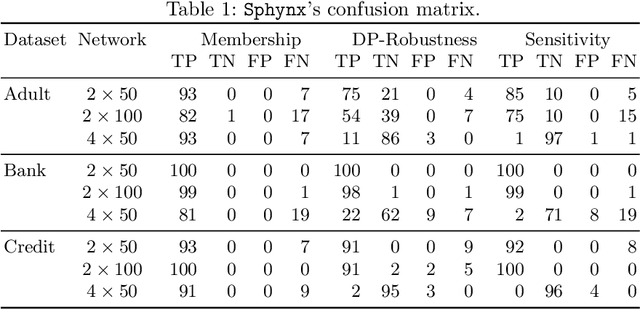

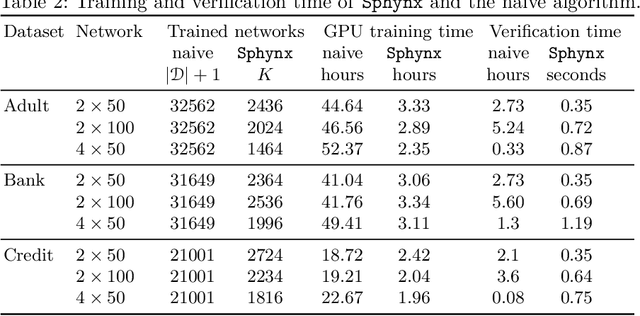
Neural networks are susceptible to privacy attacks. To date, no verifier can reason about the privacy of individuals participating in the training set. We propose a new privacy property, called local differential classification privacy (LDCP), extending local robustness to a differential privacy setting suitable for black-box classifiers. Given a neighborhood of inputs, a classifier is LDCP if it classifies all inputs the same regardless of whether it is trained with the full dataset or whether any single entry is omitted. A naive algorithm is highly impractical because it involves training a very large number of networks and verifying local robustness of the given neighborhood separately for every network. We propose Sphynx, an algorithm that computes an abstraction of all networks, with a high probability, from a small set of networks, and verifies LDCP directly on the abstract network. The challenge is twofold: network parameters do not adhere to a known distribution probability, making it difficult to predict an abstraction, and predicting too large abstraction harms the verification. Our key idea is to transform the parameters into a distribution given by KDE, allowing to keep the over-approximation error small. To verify LDCP, we extend a MILP verifier to analyze an abstract network. Experimental results show that by training only 7% of the networks, Sphynx predicts an abstract network obtaining 93% verification accuracy and reducing the analysis time by $1.7\cdot10^4$x.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge