Reducing Variance in Temporal-Difference Value Estimation via Ensemble of Deep Networks

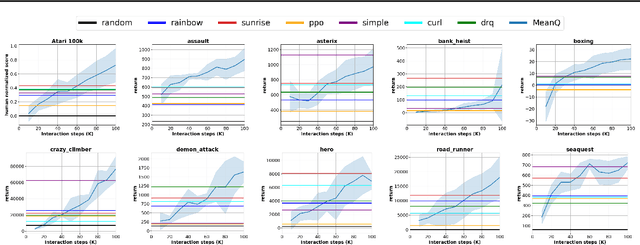
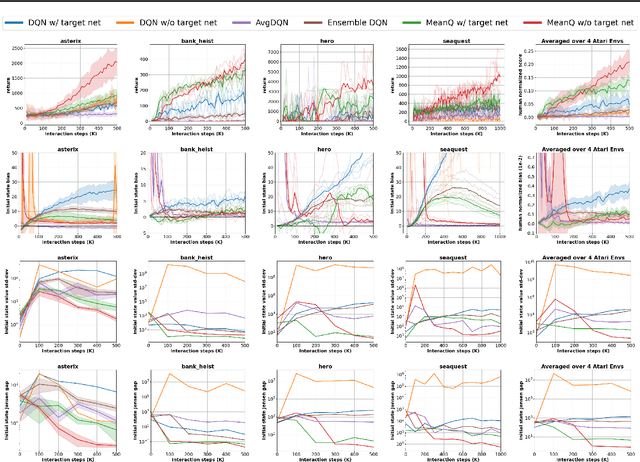
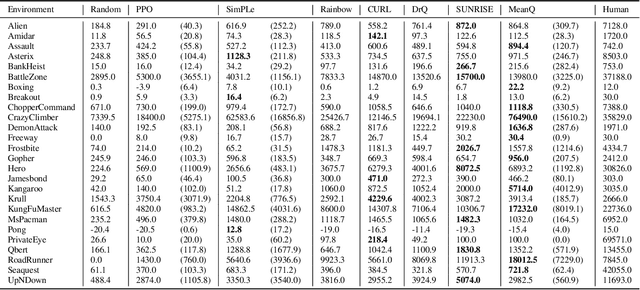
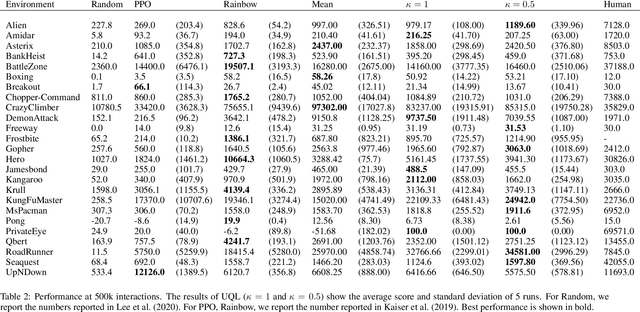
In temporal-difference reinforcement learning algorithms, variance in value estimation can cause instability and overestimation of the maximal target value. Many algorithms have been proposed to reduce overestimation, including several recent ensemble methods, however none have shown success in sample-efficient learning through addressing estimation variance as the root cause of overestimation. In this paper, we propose MeanQ, a simple ensemble method that estimates target values as ensemble means. Despite its simplicity, MeanQ shows remarkable sample efficiency in experiments on the Atari Learning Environment benchmark. Importantly, we find that an ensemble of size 5 sufficiently reduces estimation variance to obviate the lagging target network, eliminating it as a source of bias and further gaining sample efficiency. We justify intuitively and empirically the design choices in MeanQ, including the necessity of independent experience sampling. On a set of 26 benchmark Atari environments, MeanQ outperforms all tested baselines, including the best available baseline, SUNRISE, at 100K interaction steps in 16/26 environments, and by 68% on average. MeanQ also outperforms Rainbow DQN at 500K steps in 21/26 environments, and by 49% on average, and achieves average human-level performance using 200K ($\pm$100K) interaction steps. Our implementation is available at https://github.com/indylab/MeanQ.

Target Entropy Annealing for Discrete Soft Actor-Critic

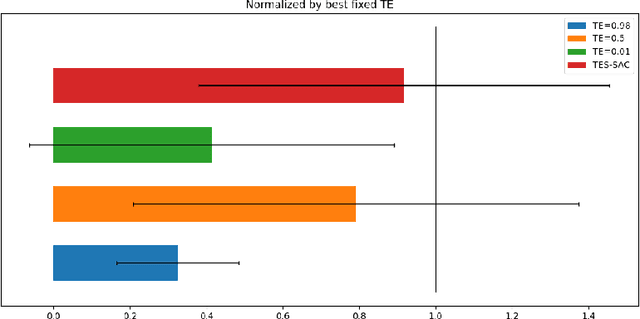
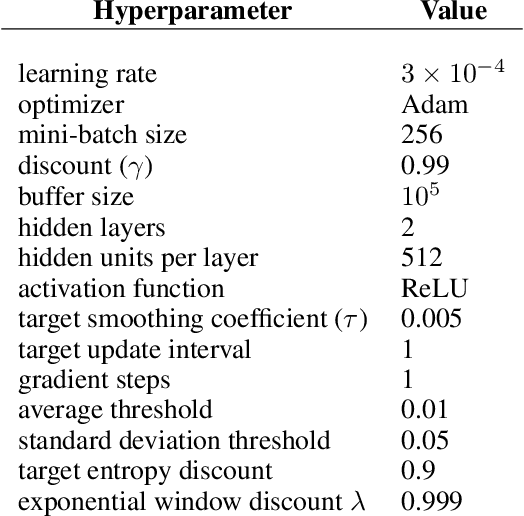
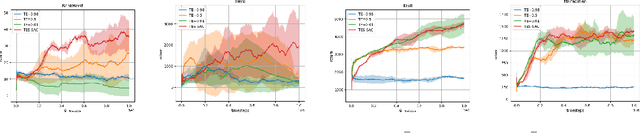
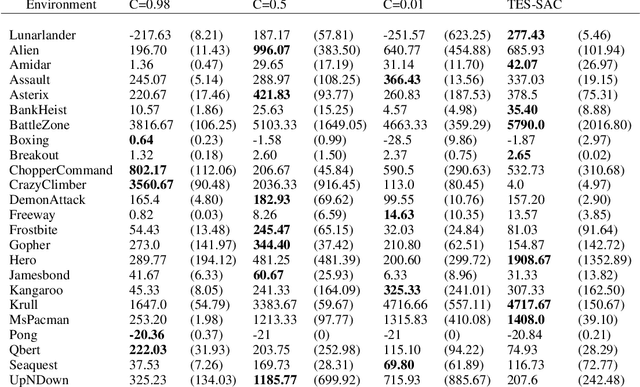
Soft Actor-Critic (SAC) is considered the state-of-the-art algorithm in continuous action space settings. It uses the maximum entropy framework for efficiency and stability, and applies a heuristic temperature Lagrange term to tune the temperature $\alpha$, which determines how "soft" the policy should be. It is counter-intuitive that empirical evidence shows SAC does not perform well in discrete domains. In this paper we investigate the possible explanations for this phenomenon and propose Target Entropy Scheduled SAC (TES-SAC), an annealing method for the target entropy parameter applied on SAC. Target entropy is a constant in the temperature Lagrange term and represents the target policy entropy in discrete SAC. We compare our method on Atari 2600 games with different constant target entropy SAC, and analyze on how our scheduling affects SAC.

Count-Based Temperature Scheduling for Maximum Entropy Reinforcement Learning

Maximum Entropy Reinforcement Learning (MaxEnt RL) algorithms such as Soft Q-Learning (SQL) and Soft Actor-Critic trade off reward and policy entropy, which has the potential to improve training stability and robustness. Most MaxEnt RL methods, however, use a constant tradeoff coefficient (temperature), contrary to the intuition that the temperature should be high early in training to avoid overfitting to noisy value estimates and decrease later in training as we increasingly trust high value estimates to truly lead to good rewards. Moreover, our confidence in value estimates is state-dependent, increasing every time we use more evidence to update an estimate. In this paper, we present a simple state-based temperature scheduling approach, and instantiate it for SQL as Count-Based Soft Q-Learning (CBSQL). We evaluate our approach on a toy domain as well as in several Atari 2600 domains and show promising results.

Temporal-Difference Value Estimation via Uncertainty-Guided Soft Updates

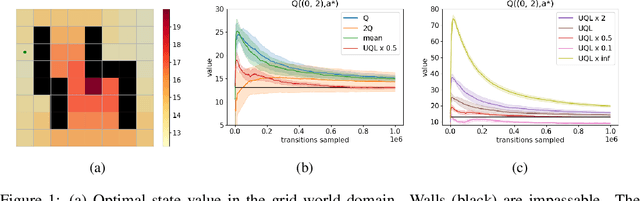
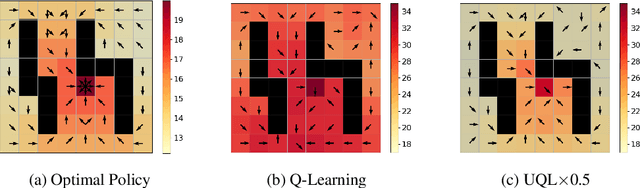
Temporal-Difference (TD) learning methods, such as Q-Learning, have proven effective at learning a policy to perform control tasks. One issue with methods like Q-Learning is that the value update introduces bias when predicting the TD target of a unfamiliar state. Estimation noise becomes a bias after the max operator in the policy improvement step, and carries over to value estimations of other states, causing Q-Learning to overestimate the Q value. Algorithms like Soft Q-Learning (SQL) introduce the notion of a soft-greedy policy, which reduces the estimation bias via soft updates in early stages of training. However, the inverse temperature $\beta$ that controls the softness of an update is usually set by a hand-designed heuristic, which can be inaccurate at capturing the uncertainty in the target estimate. Under the belief that $\beta$ is closely related to the (state dependent) model uncertainty, Entropy Regularized Q-Learning (EQL) further introduces a principled scheduling of $\beta$ by maintaining a collection of the model parameters that characterizes model uncertainty. In this paper, we present Unbiased Soft Q-Learning (UQL), which extends the work of EQL from two action, finite state spaces to multi-action, infinite state space Markov Decision Processes. We also provide a principled numerical scheduling of $\beta$, extended from SQL and using model uncertainty, during the optimization process. We show the theoretical guarantees and the effectiveness of this update method in experiments on several discrete control environments.