Temporal-Difference Value Estimation via Uncertainty-Guided Soft Updates
Paper and Code
Oct 28, 2021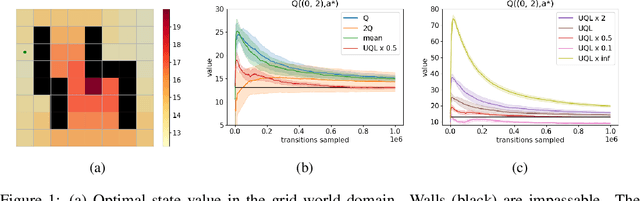

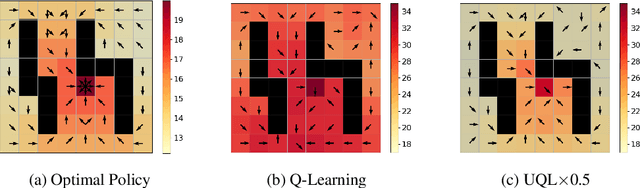
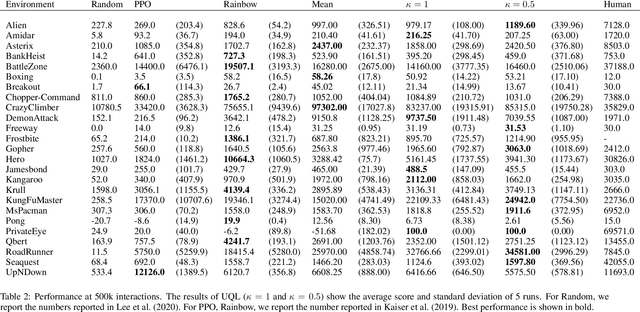
Temporal-Difference (TD) learning methods, such as Q-Learning, have proven effective at learning a policy to perform control tasks. One issue with methods like Q-Learning is that the value update introduces bias when predicting the TD target of a unfamiliar state. Estimation noise becomes a bias after the max operator in the policy improvement step, and carries over to value estimations of other states, causing Q-Learning to overestimate the Q value. Algorithms like Soft Q-Learning (SQL) introduce the notion of a soft-greedy policy, which reduces the estimation bias via soft updates in early stages of training. However, the inverse temperature $\beta$ that controls the softness of an update is usually set by a hand-designed heuristic, which can be inaccurate at capturing the uncertainty in the target estimate. Under the belief that $\beta$ is closely related to the (state dependent) model uncertainty, Entropy Regularized Q-Learning (EQL) further introduces a principled scheduling of $\beta$ by maintaining a collection of the model parameters that characterizes model uncertainty. In this paper, we present Unbiased Soft Q-Learning (UQL), which extends the work of EQL from two action, finite state spaces to multi-action, infinite state space Markov Decision Processes. We also provide a principled numerical scheduling of $\beta$, extended from SQL and using model uncertainty, during the optimization process. We show the theoretical guarantees and the effectiveness of this update method in experiments on several discrete control environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge