Tracking Temporal Dynamics of Vector Sets with Gaussian Process

Understanding the temporal evolution of sets of vectors is a fundamental challenge across various domains, including ecology, crime analysis, and linguistics. For instance, ecosystem structures evolve due to interactions among plants, herbivores, and carnivores; the spatial distribution of crimes shifts in response to societal changes; and word embedding vectors reflect cultural and semantic trends over time. However, analyzing such time-varying sets of vectors is challenging due to their complicated structures, which also evolve over time. In this work, we propose a novel method for modeling the distribution underlying each set of vectors using infinite-dimensional Gaussian processes. By approximating the latent function in the Gaussian process with Random Fourier Features, we obtain compact and comparable vector representations over time. This enables us to track and visualize temporal transitions of vector sets in a low-dimensional space. We apply our method to both sociological data (crime distributions) and linguistic data (word embeddings), demonstrating its effectiveness in capturing temporal dynamics. Our results show that the proposed approach provides interpretable and robust representations, offering a powerful framework for analyzing structural changes in temporally indexed vector sets across diverse domains.

Analyzing Continuous Semantic Shifts with Diachronic Word Similarity Matrices

The meanings and relationships of words shift over time. This phenomenon is referred to as semantic shift.Research focused on understanding how semantic shifts occur over multiple time periods is essential for gaining a detailed understanding of semantic shifts.However, detecting change points only between adjacent time periods is insufficient for analyzing detailed semantic shifts, and using BERT-based methods to examine word sense proportions incurs a high computational cost.To address those issues, we propose a simple yet intuitive framework for how semantic shifts occur over multiple time periods by leveraging a similarity matrix between the embeddings of the same word through time.We compute a diachronic word similarity matrix using fast and lightweight word embeddings across arbitrary time periods, making it deeper to analyze continuous semantic shifts.Additionally, by clustering the similarity matrices for different words, we can categorize words that exhibit similar behavior of semantic shift in an unsupervised manner.

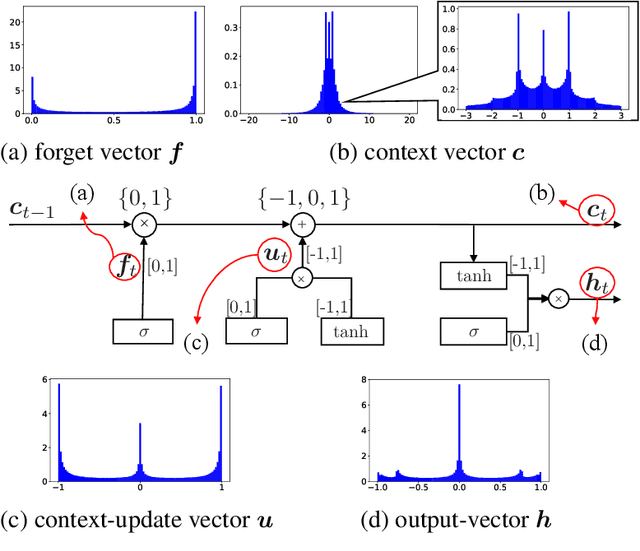
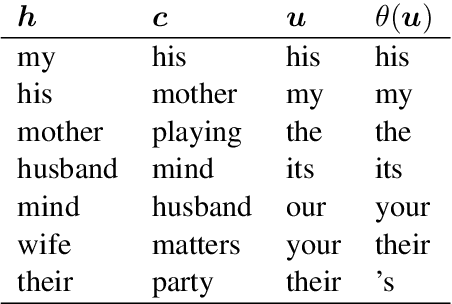
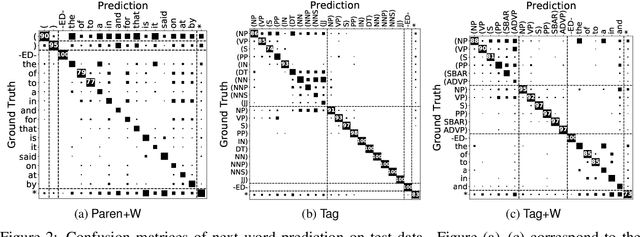
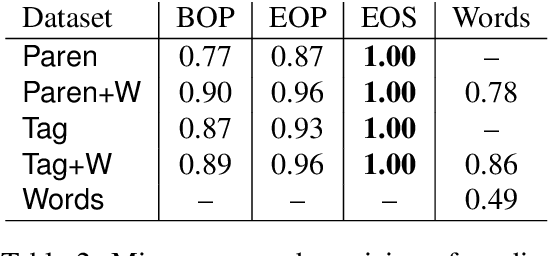
How LSTM Encodes Syntax: Exploring Context Vectors and Semi-Quantization on Natural Text

Long Short-Term Memory recurrent neural network (LSTM) is widely used and known to capture informative long-term syntactic dependencies. However, how such information are reflected in its internal vectors for natural text has not yet been sufficiently investigated. We analyze them by learning a language model where syntactic structures are implicitly given. We empirically show that the context update vectors, i.e. outputs of internal gates, are approximately quantized to binary or ternary values to help the language model to count the depth of nesting accurately, as Suzgun et al. (2019) recently show for synthetic Dyck languages. For some dimensions in the context vector, we show that their activations are highly correlated with the depth of phrase structures, such as VP and NP. Moreover, with an $L_1$ regularization, we also found that it can accurately predict whether a word is inside a phrase structure or not from a small number of components of the context vector. Even for the case of learning from raw text, context vectors are shown to still correlate well with the phrase structures. Finally, we show that natural clusters of the functional words and the part of speeches that trigger phrases are represented in a small but principal subspace of the context-update vector of LSTM.

Restricted Collapsed Draw: Accurate Sampling for Hierarchical Chinese Restaurant Process Hidden Markov Models

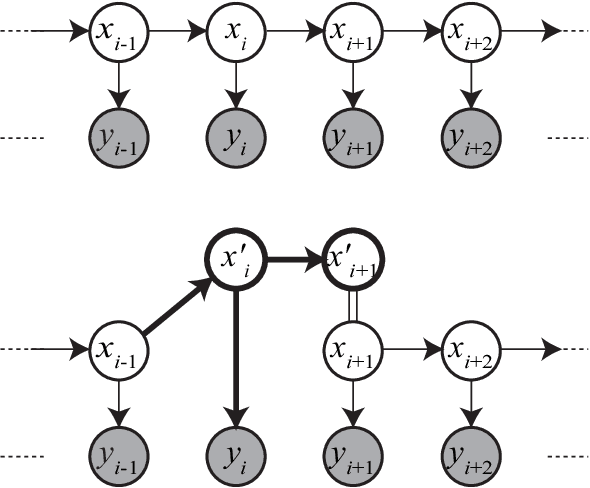
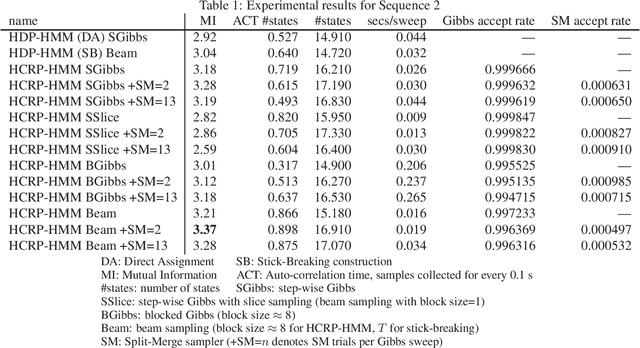
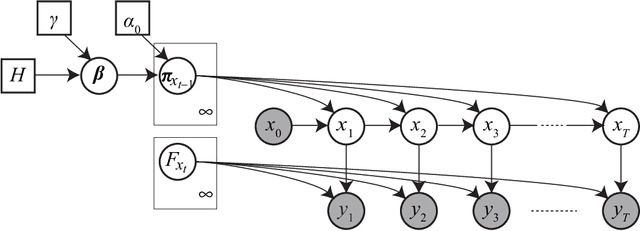
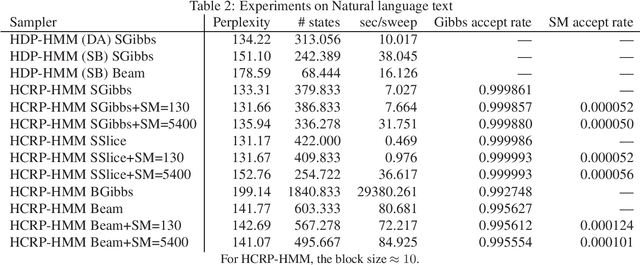
We propose a restricted collapsed draw (RCD) sampler, a general Markov chain Monte Carlo sampler of simultaneous draws from a hierarchical Chinese restaurant process (HCRP) with restriction. Models that require simultaneous draws from a hierarchical Dirichlet process with restriction, such as infinite Hidden markov models (iHMM), were difficult to enjoy benefits of \markerg{the} HCRP due to combinatorial explosion in calculating distributions of coupled draws. By constructing a proposal of seating arrangements (partitioning) and stochastically accepts the proposal by the Metropolis-Hastings algorithm, the RCD sampler makes accurate sampling for complex combination of draws while retaining efficiency of HCRP representation. Based on the RCD sampler, we developed a series of sophisticated sampling algorithms for iHMMs, including blocked Gibbs sampling, beam sampling, and split-merge sampling, that outperformed conventional iHMM samplers in experiments