Wasserstein Gradient Flow over Variational Parameter Space for Variational Inference

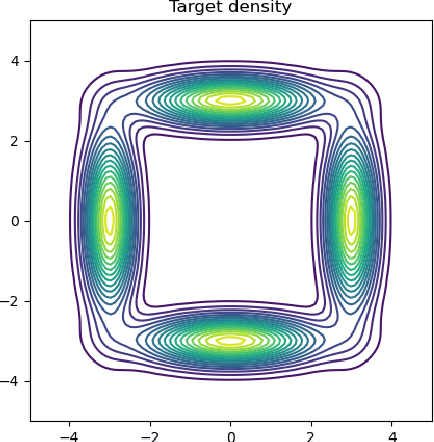
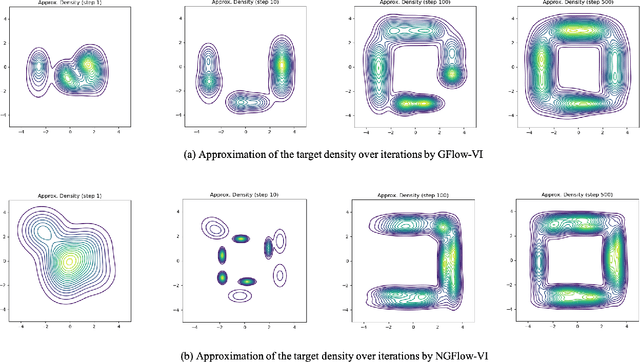
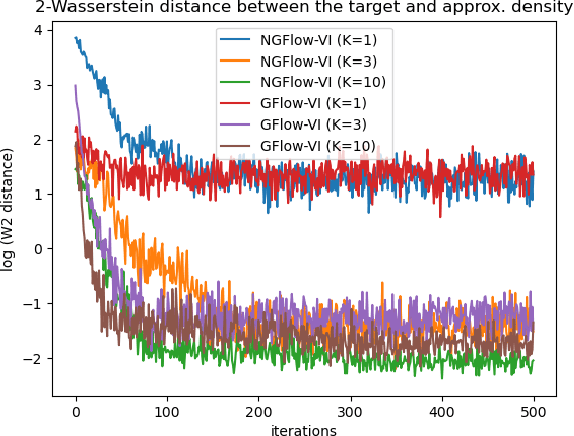
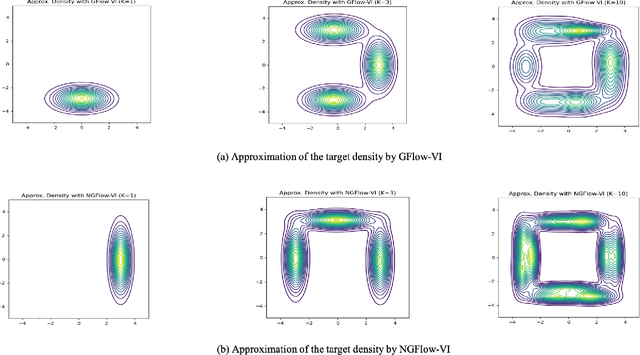
Variational inference (VI) can be cast as an optimization problem in which the variational parameters are tuned to closely align a variational distribution with the true posterior. The optimization task can be approached through vanilla gradient descent in black-box VI or natural-gradient descent in natural-gradient VI. In this work, we reframe VI as the optimization of an objective that concerns probability distributions defined over a \textit{variational parameter space}. Subsequently, we propose Wasserstein gradient descent for tackling this optimization problem. Notably, the optimization techniques, namely black-box VI and natural-gradient VI, can be reinterpreted as specific instances of the proposed Wasserstein gradient descent. To enhance the efficiency of optimization, we develop practical methods for numerically solving the discrete gradient flows. We validate the effectiveness of the proposed methods through empirical experiments on a synthetic dataset, supplemented by theoretical analyses.

Moreau-Yoshida Variational Transport: A General Framework For Solving Regularized Distributional Optimization Problems

We consider a general optimization problem of minimizing a composite objective functional defined over a class of probability distributions. The objective is composed of two functionals: one is assumed to possess the variational representation and the other is expressed in terms of the expectation operator of a possibly nonsmooth convex regularizer function. Such a regularized distributional optimization problem widely appears in machine learning and statistics, such as proximal Monte-Carlo sampling, Bayesian inference and generative modeling, for regularized estimation and generation. We propose a novel method, dubbed as Moreau-Yoshida Variational Transport (MYVT), for solving the regularized distributional optimization problem. First, as the name suggests, our method employs the Moreau-Yoshida envelope for a smooth approximation of the nonsmooth function in the objective. Second, we reformulate the approximate problem as a concave-convex saddle point problem by leveraging the variational representation, and then develope an efficient primal-dual algorithm to approximate the saddle point. Furthermore, we provide theoretical analyses and report experimental results to demonstrate the effectiveness of the proposed method.

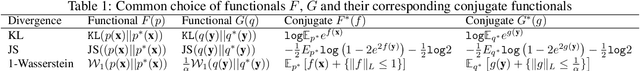
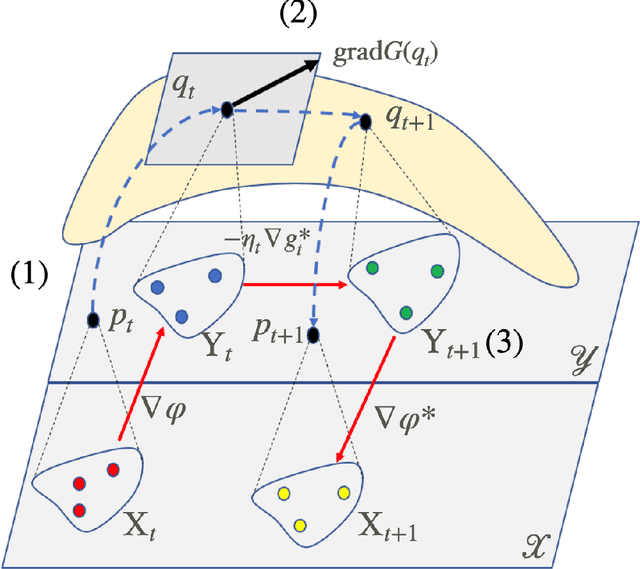
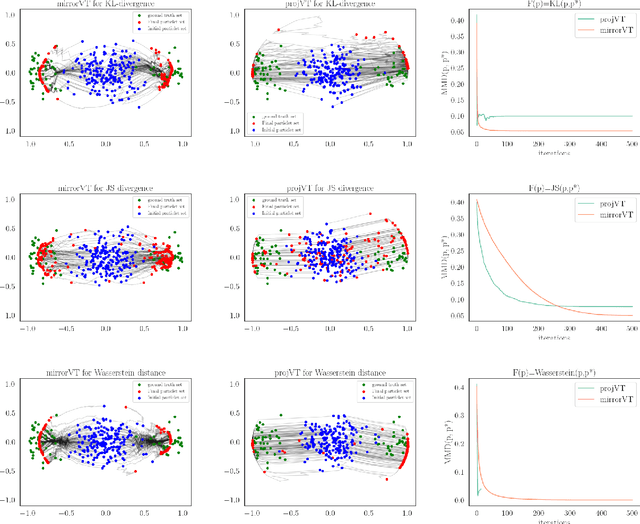
A Particle-Based Algorithm for Distributional Optimization on \textit{Constrained Domains} via Variational Transport and Mirror Descent

We consider the optimization problem of minimizing an objective functional, which admits a variational form and is defined over probability distributions on the constrained domain, which poses challenges to both theoretical analysis and algorithmic design. Inspired by the mirror descent algorithm for constrained optimization, we propose an iterative particle-based algorithm, named Mirrored Variational Transport (mirrorVT), extended from the Variational Transport framework [7] for dealing with the constrained domain. In particular, for each iteration, mirrorVT maps particles to an unconstrained dual domain induced by a mirror map and then approximately perform Wasserstein gradient descent on the manifold of distributions defined over the dual space by pushing particles. At the end of iteration, particles are mapped back to the original constrained domain. Through simulated experiments, we demonstrate the effectiveness of mirrorVT for minimizing the functionals over probability distributions on the simplex- and Euclidean ball-constrained domains. We also analyze its theoretical properties and characterize its convergence to the global minimum of the objective functional.

On a linear fused Gromov-Wasserstein distance for graph structured data

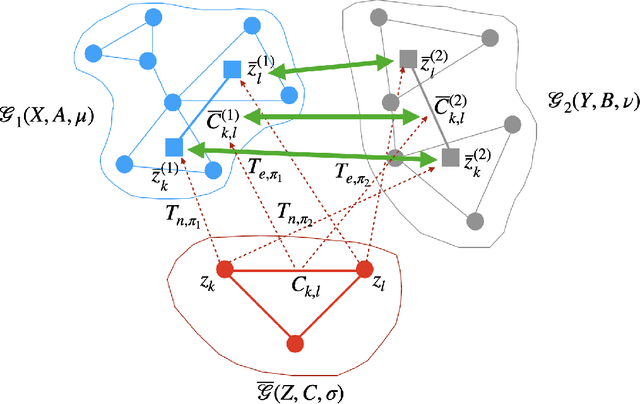
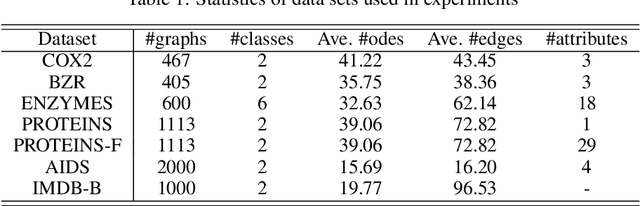
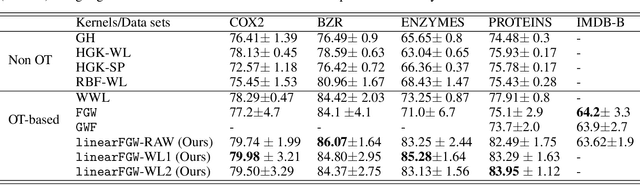
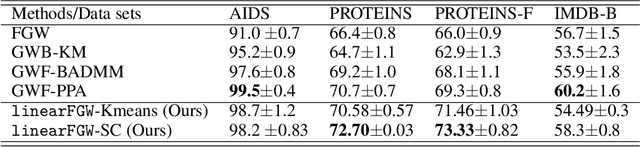
We present a framework for embedding graph structured data into a vector space, taking into account node features and topology of a graph into the optimal transport (OT) problem. Then we propose a novel distance between two graphs, named linearFGW, defined as the Euclidean distance between their embeddings. The advantages of the proposed distance are twofold: 1) it can take into account node feature and structure of graphs for measuring the similarity between graphs in a kernel-based framework, 2) it can be much faster for computing kernel matrix than pairwise OT-based distances, particularly fused Gromov-Wasserstein, making it possible to deal with large-scale data sets. After discussing theoretical properties of linearFGW, we demonstrate experimental results on classification and clustering tasks, showing the effectiveness of the proposed linearFGW.

Learning subtree pattern importance for Weisfeiler-Lehmanbased graph kernels

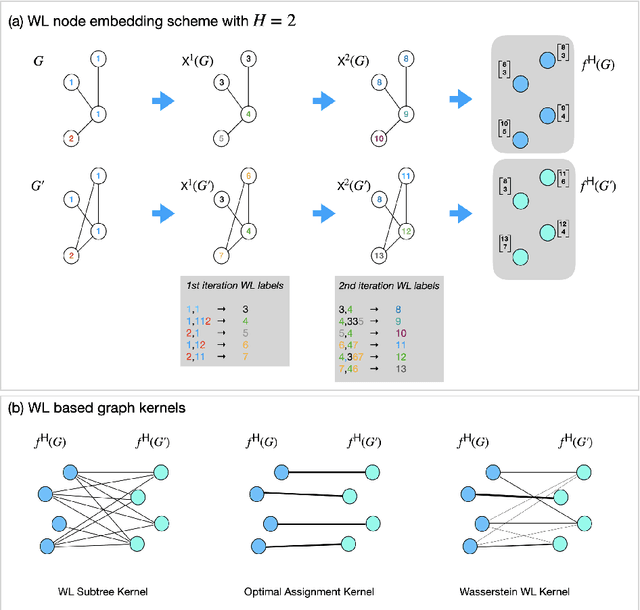
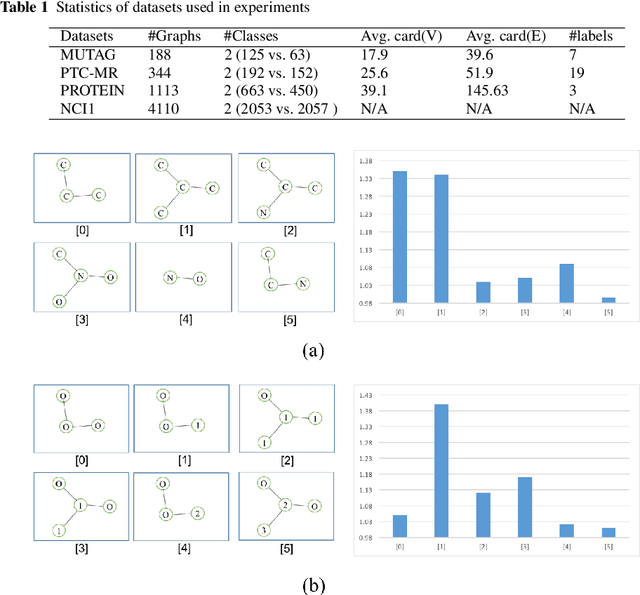
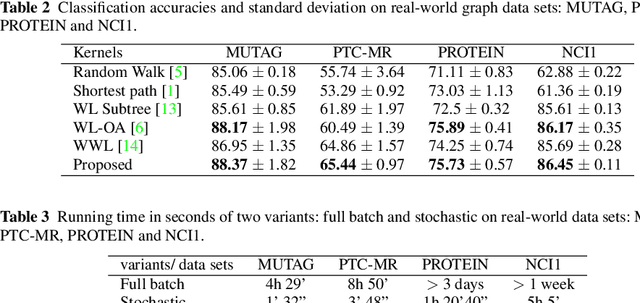
Graph is an usual representation of relational data, which are ubiquitous in manydomains such as molecules, biological and social networks. A popular approach to learningwith graph structured data is to make use of graph kernels, which measure the similaritybetween graphs and are plugged into a kernel machine such as a support vector machine.Weisfeiler-Lehman (WL) based graph kernels, which employ WL labeling scheme to extract subtree patterns and perform node embedding, are demonstrated to achieve great performance while being efficiently computable. However, one of the main drawbacks of ageneral kernel is the decoupling of kernel construction and learning process. For moleculargraphs, usual kernels such as WL subtree, based on substructures of the molecules, consider all available substructures having the same importance, which might not be suitable inpractice. In this paper, we propose a method to learn the weights of subtree patterns in the framework of WWL kernels, the state of the art method for graph classification task [14]. To overcome the computational issue on large scale data sets, we present an efficient learning algorithm and also derive a generalization gap bound to show its convergence. Finally, through experiments on synthetic and real-world data sets, we demonstrate the effectiveness of our proposed method for learning the weights of subtree patterns.

A generative model for molecule generation based on chemical reaction trees

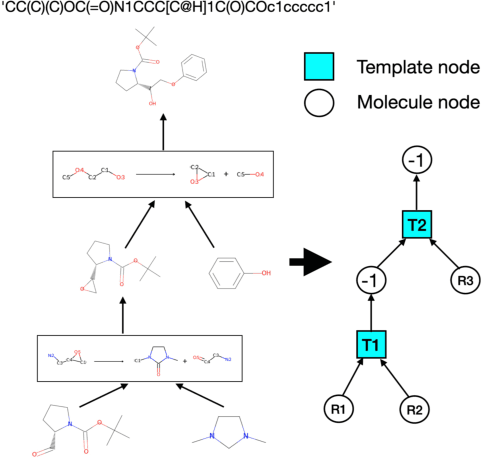
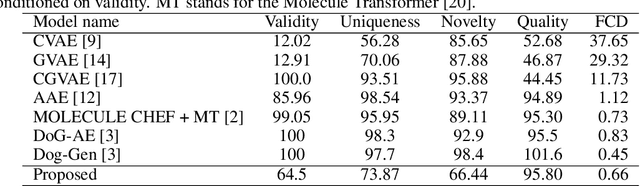
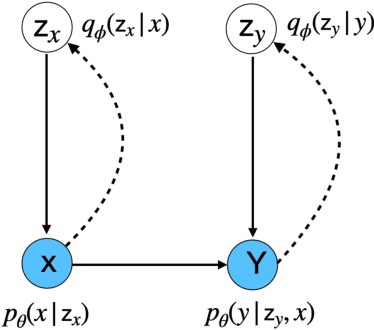
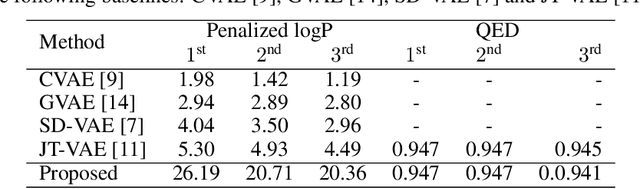
Deep generative models have been shown powerful in generating novel molecules with desired chemical properties via their representations such as strings, trees or graphs. However, these models are limited in recommending synthetic routes for the generated molecules in practice. We propose a generative model to generate molecules via multi-step chemical reaction trees. Specifically, our model first propose a chemical reaction tree with predicted reaction templates and commercially available molecules (starting molecules), and then perform forward synthetic steps to obtain product molecules. Experiments show that our model can generate chemical reactions whose product molecules are with desired chemical properties. Also, the complete synthetic routes for these product molecules are provided.