Semi-supervised Learning on Large Graphs: is Poisson Learning a Game-Changer?

We explain Poisson learning on graph-based semi-supervised learning to see if it could avoid the problem of global information loss problem as Laplace-based learning methods on large graphs. From our analysis, Poisson learning is simply Laplace regularization with thresholding, cannot overcome the problem.

CentSmoothie: Central-Smoothing Hypergraph Neural Networks for Predicting Drug-Drug Interactions

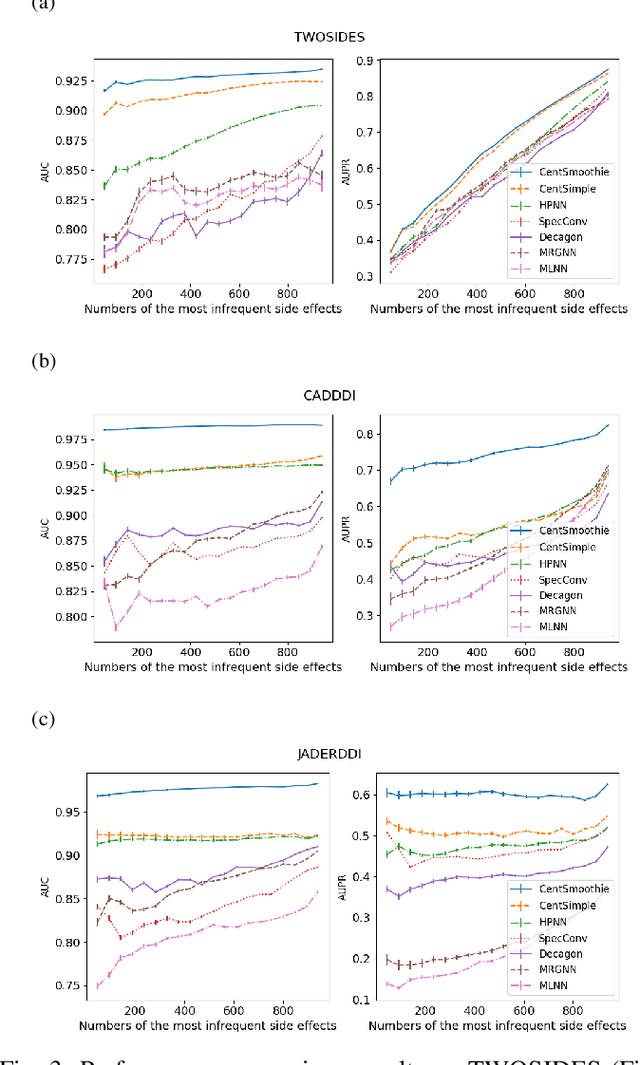
Predicting drug-drug interactions (DDI) is the problem of predicting side effects (unwanted outcomes) of a pair of drugs using drug information and known side effects of many pairs. This problem can be formulated as predicting labels (i.e. side effects) for each pair of nodes in a DDI graph, of which nodes are drugs and edges are interacting drugs with known labels. State-of-the-art methods for this problem are graph neural networks (GNNs), which leverage neighborhood information in the graph to learn node representations. For DDI, however, there are many labels with complicated relationships due to the nature of side effects. Usual GNNs often fix labels as one-hot vectors that do not reflect label relationships and potentially do not obtain the highest performance in the difficult cases of infrequent labels. In this paper, we formulate DDI as a hypergraph where each hyperedge is a triple: two nodes for drugs and one node for a label. We then present CentSmoothie, a hypergraph neural network that learns representations of nodes and labels altogether with a novel central-smoothing formulation. We empirically demonstrate the performance advantages of CentSmoothie in simulations as well as real datasets.

Learning subtree pattern importance for Weisfeiler-Lehmanbased graph kernels

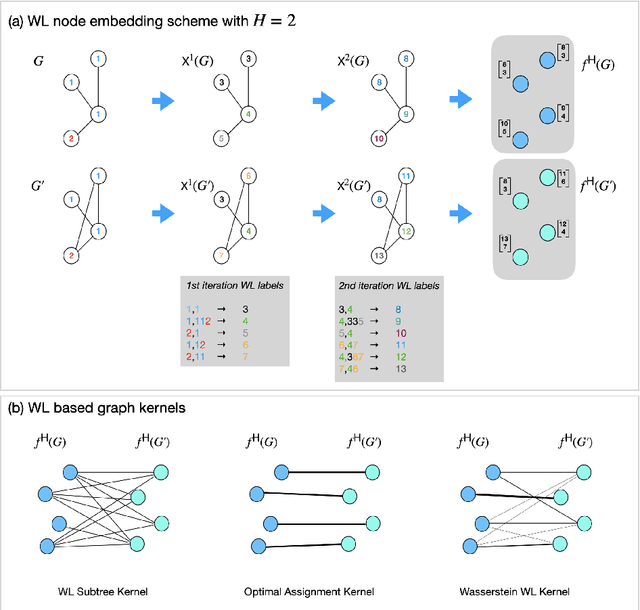
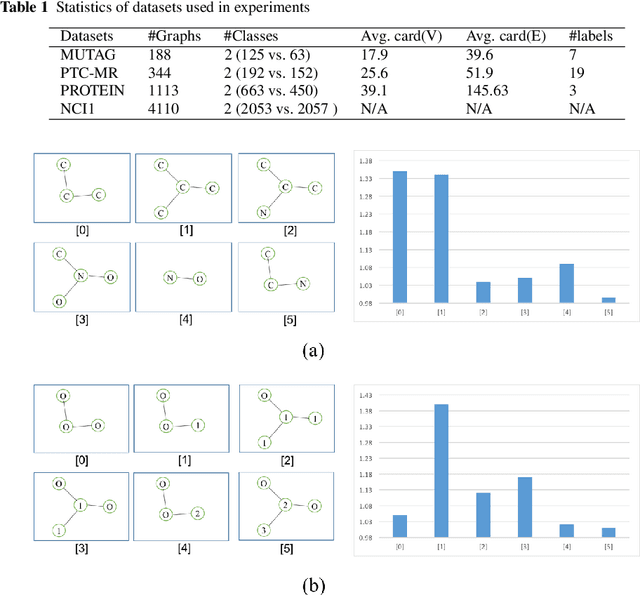
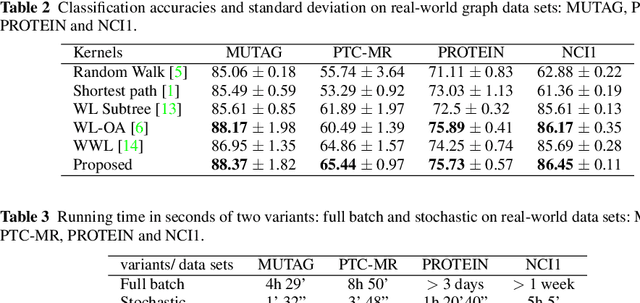
Graph is an usual representation of relational data, which are ubiquitous in manydomains such as molecules, biological and social networks. A popular approach to learningwith graph structured data is to make use of graph kernels, which measure the similaritybetween graphs and are plugged into a kernel machine such as a support vector machine.Weisfeiler-Lehman (WL) based graph kernels, which employ WL labeling scheme to extract subtree patterns and perform node embedding, are demonstrated to achieve great performance while being efficiently computable. However, one of the main drawbacks of ageneral kernel is the decoupling of kernel construction and learning process. For moleculargraphs, usual kernels such as WL subtree, based on substructures of the molecules, consider all available substructures having the same importance, which might not be suitable inpractice. In this paper, we propose a method to learn the weights of subtree patterns in the framework of WWL kernels, the state of the art method for graph classification task [14]. To overcome the computational issue on large scale data sets, we present an efficient learning algorithm and also derive a generalization gap bound to show its convergence. Finally, through experiments on synthetic and real-world data sets, we demonstrate the effectiveness of our proposed method for learning the weights of subtree patterns.

On Convex Clustering Solutions

Convex clustering is an attractive clustering algorithm with favorable properties such as efficiency and optimality owing to its convex formulation. It is thought to generalize both k-means clustering and agglomerative clustering. However, it is not known whether convex clustering preserves desirable properties of these algorithms. A common expectation is that convex clustering may learn difficult cluster types such as non-convex ones. Current understanding of convex clustering is limited to only consistency results on well-separated clusters. We show new understanding of its solutions. We prove that convex clustering can only learn convex clusters. We then show that the clusters have disjoint bounding balls with significant gaps. We further characterize the solutions, regularization hyperparameters, inclusterable cases and consistency.

Learning on Hypergraphs with Sparsity

Hypergraph is a general way of representing high-order relations on a set of objects. It is a generalization of graph, in which only pairwise relations can be represented. It finds applications in various domains where relationships of more than two objects are observed. On a hypergraph, as a generalization of graph, one wishes to learn a smooth function with respect to its topology. A fundamental issue is to find suitable smoothness measures of functions on the nodes of a graph/hypergraph. We show a general framework that generalizes previously proposed smoothness measures and also gives rise to new ones. To address the problem of irrelevant or noisy data, we wish to incorporate sparse learning framework into learning on hypergraphs. We propose sparsely smooth formulations that learn smooth functions and induce sparsity on hypergraphs at both hyperedge and node levels. We show their properties and sparse support recovery results. We conduct experiments to show that our sparsely smooth models have benefits to irrelevant and noisy data, and usually give similar or improved performances compared to dense models.