Wasserstein Gradient Flow over Variational Parameter Space for Variational Inference
Paper and Code
Oct 25, 2023
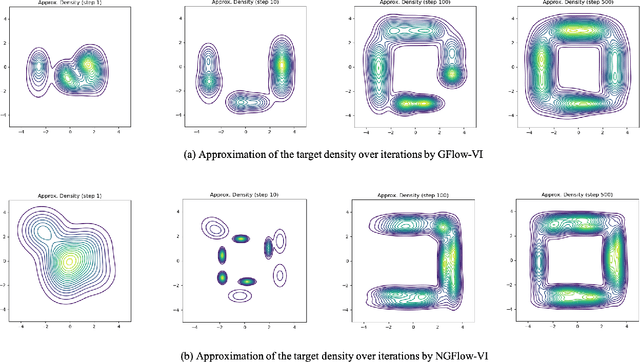
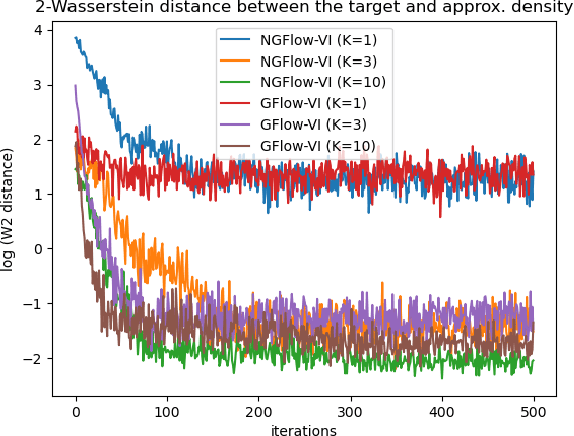
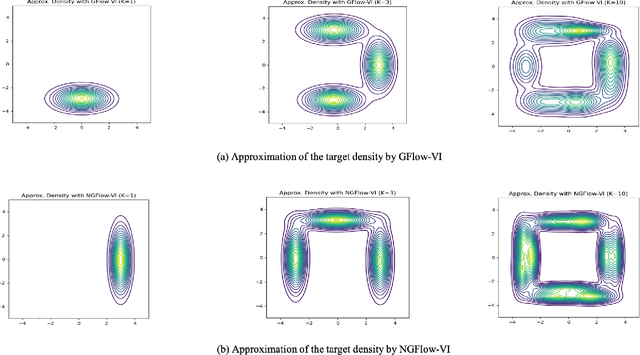
Variational inference (VI) can be cast as an optimization problem in which the variational parameters are tuned to closely align a variational distribution with the true posterior. The optimization task can be approached through vanilla gradient descent in black-box VI or natural-gradient descent in natural-gradient VI. In this work, we reframe VI as the optimization of an objective that concerns probability distributions defined over a \textit{variational parameter space}. Subsequently, we propose Wasserstein gradient descent for tackling this optimization problem. Notably, the optimization techniques, namely black-box VI and natural-gradient VI, can be reinterpreted as specific instances of the proposed Wasserstein gradient descent. To enhance the efficiency of optimization, we develop practical methods for numerically solving the discrete gradient flows. We validate the effectiveness of the proposed methods through empirical experiments on a synthetic dataset, supplemented by theoretical analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge