Continual Reinforcement Learning with TELLA

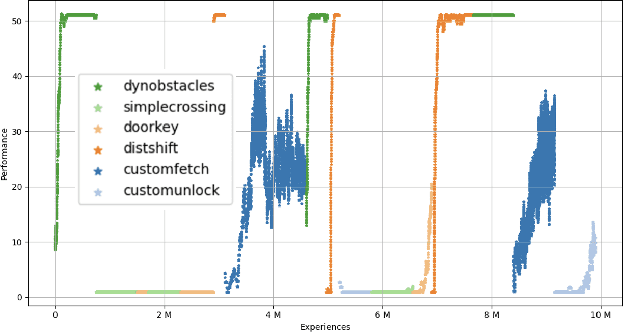
Training reinforcement learning agents that continually learn across multiple environments is a challenging problem. This is made more difficult by a lack of reproducible experiments and standard metrics for comparing different continual learning approaches. To address this, we present TELLA, a tool for the Test and Evaluation of Lifelong Learning Agents. TELLA provides specified, reproducible curricula to lifelong learning agents while logging detailed data for evaluation and standardized analysis. Researchers can define and share their own curricula over various learning environments or run against a curriculum created under the DARPA Lifelong Learning Machines (L2M) Program.

Geometric instability of out of distribution data across autoencoder architecture

We study the map learned by a family of autoencoders trained on MNIST, and evaluated on ten different data sets created by the random selection of pixel values according to ten different distributions. Specifically, we study the eigenvalues of the Jacobians defined by the weight matrices of the autoencoder at each training and evaluation point. For high enough latent dimension, we find that each autoencoder reconstructs all the evaluation data sets as similar \emph{generalized characters}, but that this reconstructed \emph{generalized character} changes across autoencoder. Eigenvalue analysis shows that even when the reconstructed image appears to be an MNIST character for all out of distribution data sets, not all have latent representations that are close to the latent representation of MNIST characters. All told, the eigenvalue analysis demonstrated a great deal of geometric instability of the autoencoder both as a function on out of distribution inputs, and across architectures on the same set of inputs.

Eigenvalues of Autoencoders in Training and at Initialization

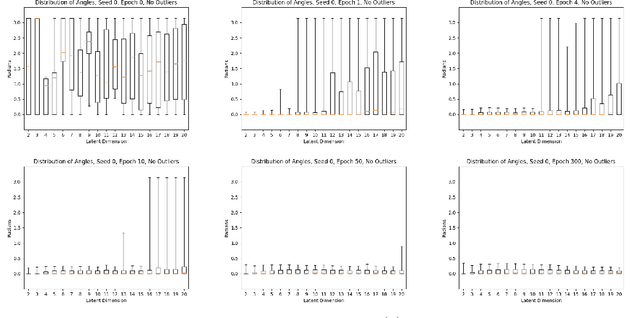
In this paper, we investigate the evolution of autoencoders near their initialization. In particular, we study the distribution of the eigenvalues of the Jacobian matrices of autoencoders early in the training process, training on the MNIST data set. We find that autoencoders that have not been trained have eigenvalue distributions that are qualitatively different from those which have been trained for a long time ($>$100 epochs). Additionally, we find that even at early epochs, these eigenvalue distributions rapidly become qualitatively similar to those of the fully trained autoencoders. We also compare the eigenvalues at initialization to pertinent theoretical work on the eigenvalues of random matrices and the products of such matrices.

Instructive artificial intelligence (AI) for human training, assistance, and explainability

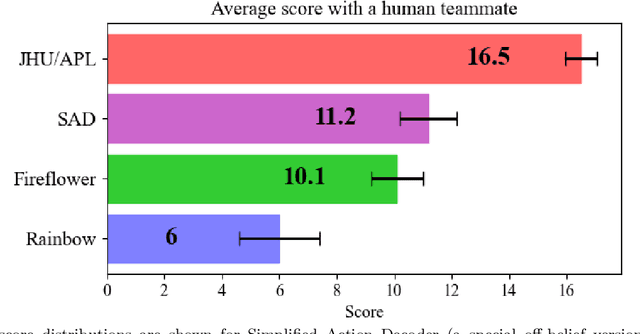
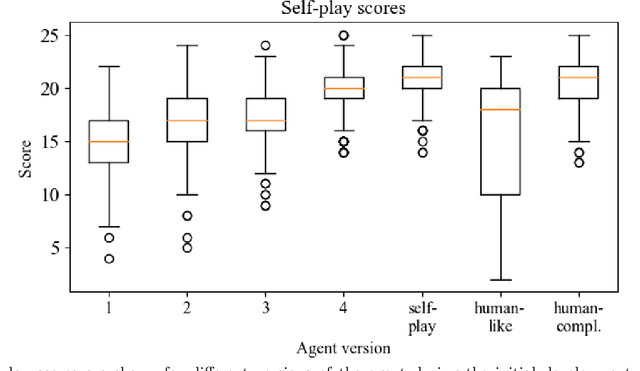
We propose a novel approach to explainable AI (XAI) based on the concept of "instruction" from neural networks. In this case study, we demonstrate how a superhuman neural network might instruct human trainees as an alternative to traditional approaches to XAI. Specifically, an AI examines human actions and calculates variations on the human strategy that lead to better performance. Experiments with a JHU/APL-developed AI player for the cooperative card game Hanabi suggest this technique makes unique contributions to explainability while improving human performance. One area of focus for Instructive AI is in the significant discrepancies that can arise between a human's actual strategy and the strategy they profess to use. This inaccurate self-assessment presents a barrier for XAI, since explanations of an AI's strategy may not be properly understood or implemented by human recipients. We have developed and are testing a novel, Instructive AI approach that estimates human strategy by observing human actions. With neural networks, this allows a direct calculation of the changes in weights needed to improve the human strategy to better emulate a more successful AI. Subjected to constraints (e.g. sparsity) these weight changes can be interpreted as recommended changes to human strategy (e.g. "value A more, and value B less"). Instruction from AI such as this functions both to help humans perform better at tasks, but also to better understand, anticipate, and correct the actions of an AI. Results will be presented on AI instruction's ability to improve human decision-making and human-AI teaming in Hanabi.

Geometry and Generalization: Eigenvalues as predictors of where a network will fail to generalize

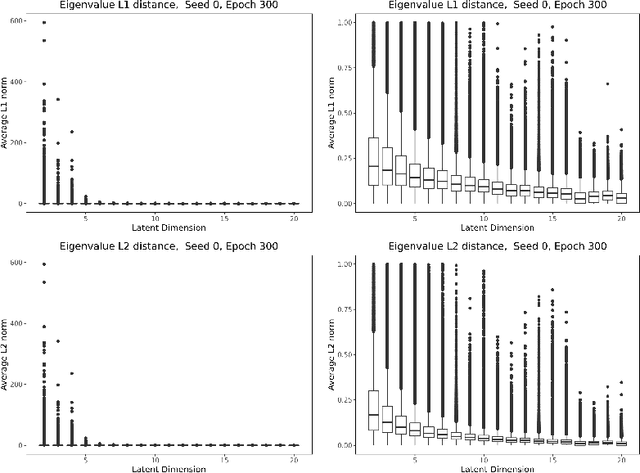
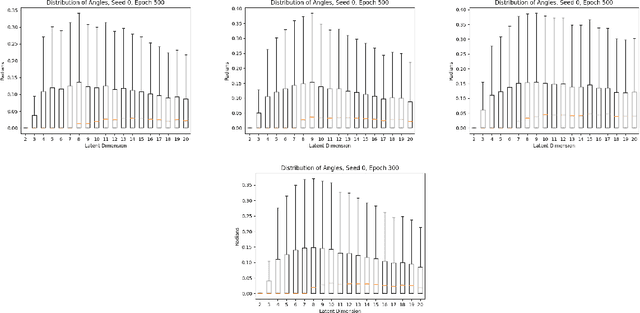
We study the deformation of the input space by a trained autoencoder via the Jacobians of the trained weight matrices. In doing so, we prove bounds for the mean squared errors for points in the input space, under assumptions regarding the orthogonality of the eigenvectors. We also show that the trace and the product of the eigenvalues of the Jacobian matrices is a good predictor of the MSE on test points. This is a dataset independent means of testing an autoencoder's ability to generalize on new input. Namely, no knowledge of the dataset on which the network was trained is needed, only the parameters of the trained model.