Structural Similarity for Improved Transfer in Reinforcement Learning

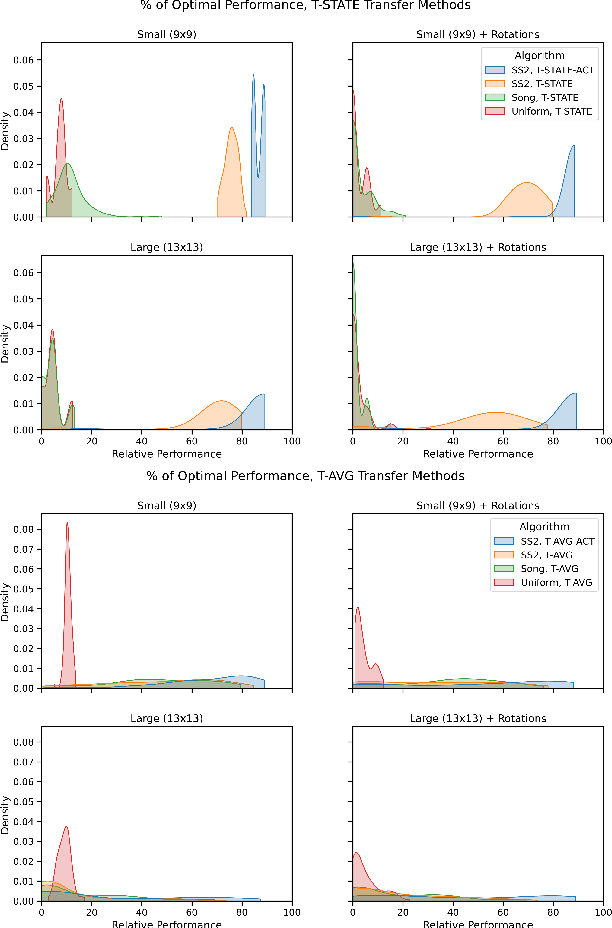
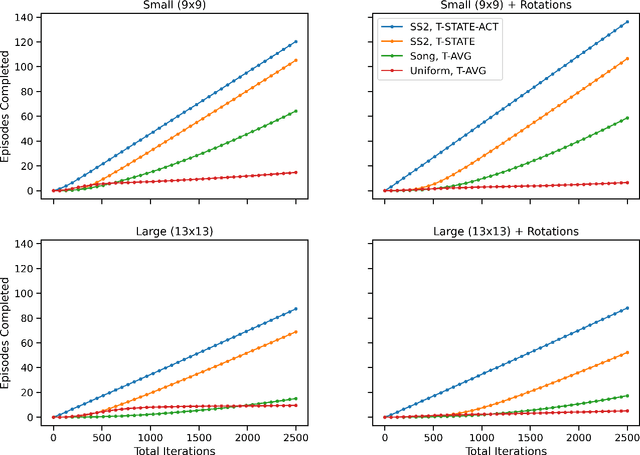
Transfer learning is an increasingly common approach for developing performant RL agents. However, it is not well understood how to define the relationship between the source and target tasks, and how this relationship contributes to successful transfer. We present an algorithm called Structural Similarity for Two MDPS, or SS2, that calculates a state similarity measure for states in two finite MDPs based on previously developed bisimulation metrics, and show that the measure satisfies properties of a distance metric. Then, through empirical results with GridWorld navigation tasks, we provide evidence that the distance measure can be used to improve transfer performance for Q-Learning agents over previous implementations.

Geometric instability of out of distribution data across autoencoder architecture

We study the map learned by a family of autoencoders trained on MNIST, and evaluated on ten different data sets created by the random selection of pixel values according to ten different distributions. Specifically, we study the eigenvalues of the Jacobians defined by the weight matrices of the autoencoder at each training and evaluation point. For high enough latent dimension, we find that each autoencoder reconstructs all the evaluation data sets as similar \emph{generalized characters}, but that this reconstructed \emph{generalized character} changes across autoencoder. Eigenvalue analysis shows that even when the reconstructed image appears to be an MNIST character for all out of distribution data sets, not all have latent representations that are close to the latent representation of MNIST characters. All told, the eigenvalue analysis demonstrated a great deal of geometric instability of the autoencoder both as a function on out of distribution inputs, and across architectures on the same set of inputs.

Eigenvalues of Autoencoders in Training and at Initialization

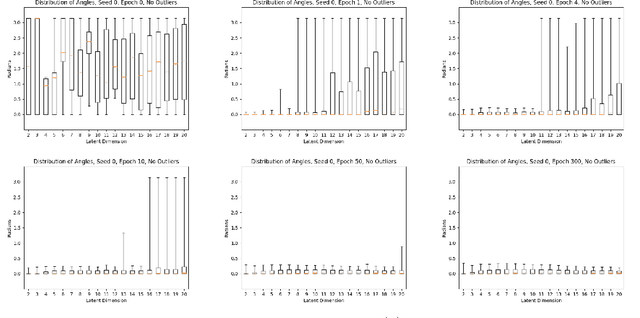
In this paper, we investigate the evolution of autoencoders near their initialization. In particular, we study the distribution of the eigenvalues of the Jacobian matrices of autoencoders early in the training process, training on the MNIST data set. We find that autoencoders that have not been trained have eigenvalue distributions that are qualitatively different from those which have been trained for a long time ($>$100 epochs). Additionally, we find that even at early epochs, these eigenvalue distributions rapidly become qualitatively similar to those of the fully trained autoencoders. We also compare the eigenvalues at initialization to pertinent theoretical work on the eigenvalues of random matrices and the products of such matrices.

Geometry and Generalization: Eigenvalues as predictors of where a network will fail to generalize

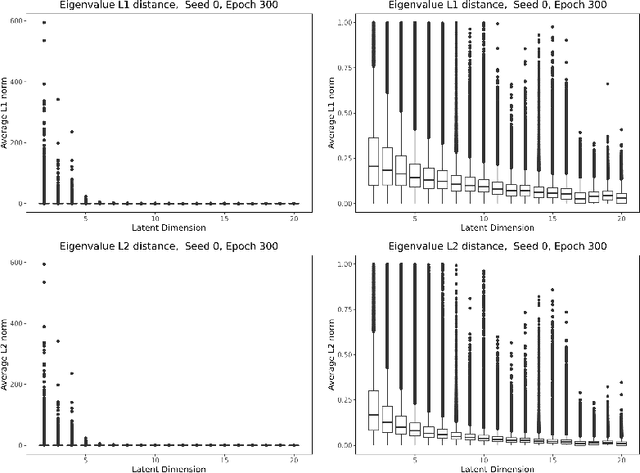
We study the deformation of the input space by a trained autoencoder via the Jacobians of the trained weight matrices. In doing so, we prove bounds for the mean squared errors for points in the input space, under assumptions regarding the orthogonality of the eigenvectors. We also show that the trace and the product of the eigenvalues of the Jacobian matrices is a good predictor of the MSE on test points. This is a dataset independent means of testing an autoencoder's ability to generalize on new input. Namely, no knowledge of the dataset on which the network was trained is needed, only the parameters of the trained model.