Eigenvalues of Autoencoders in Training and at Initialization

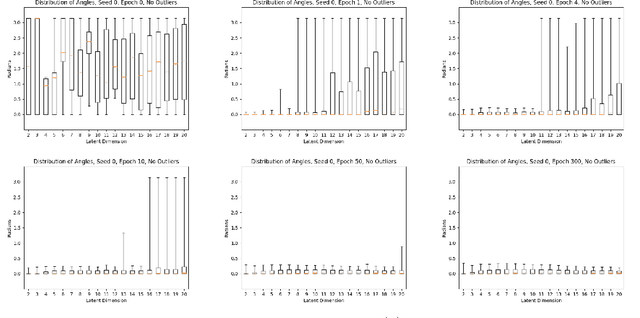
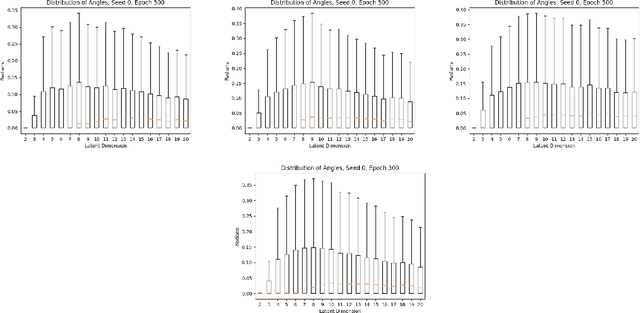
In this paper, we investigate the evolution of autoencoders near their initialization. In particular, we study the distribution of the eigenvalues of the Jacobian matrices of autoencoders early in the training process, training on the MNIST data set. We find that autoencoders that have not been trained have eigenvalue distributions that are qualitatively different from those which have been trained for a long time ($>$100 epochs). Additionally, we find that even at early epochs, these eigenvalue distributions rapidly become qualitatively similar to those of the fully trained autoencoders. We also compare the eigenvalues at initialization to pertinent theoretical work on the eigenvalues of random matrices and the products of such matrices.

Geometry and Generalization: Eigenvalues as predictors of where a network will fail to generalize

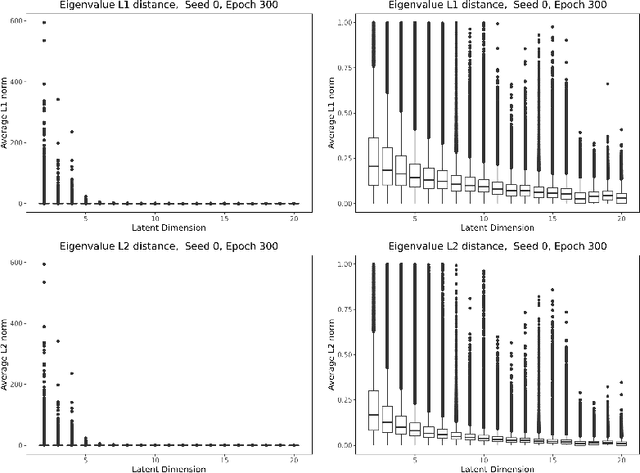
We study the deformation of the input space by a trained autoencoder via the Jacobians of the trained weight matrices. In doing so, we prove bounds for the mean squared errors for points in the input space, under assumptions regarding the orthogonality of the eigenvectors. We also show that the trace and the product of the eigenvalues of the Jacobian matrices is a good predictor of the MSE on test points. This is a dataset independent means of testing an autoencoder's ability to generalize on new input. Namely, no knowledge of the dataset on which the network was trained is needed, only the parameters of the trained model.