Interpretability in Safety-Critical FinancialTrading Systems

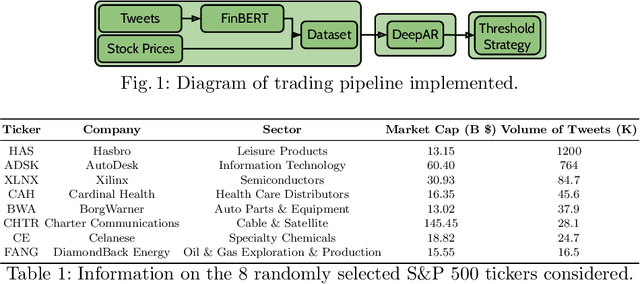
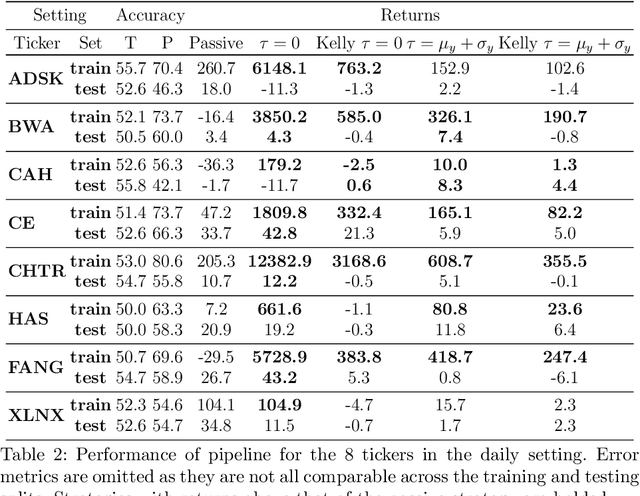
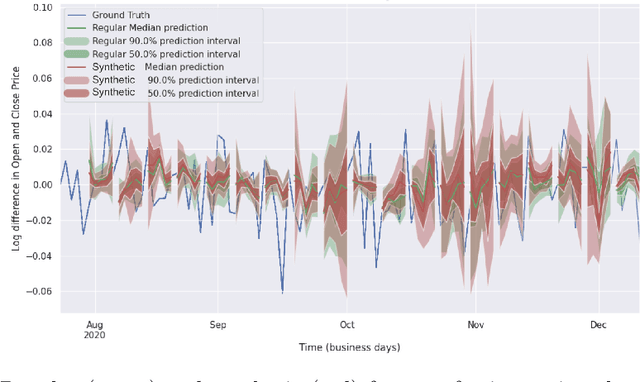
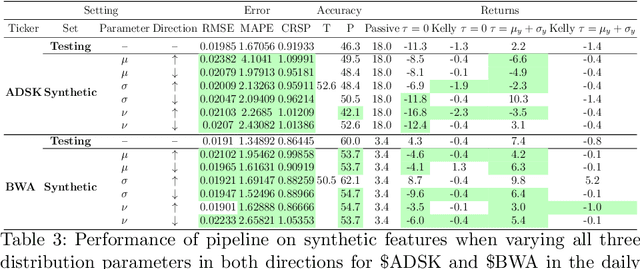
Sophisticated machine learning (ML) models to inform trading in the financial sector create problems of interpretability and risk management. Seemingly robust forecasting models may behave erroneously in out of distribution settings. In 2020, some of the world's most sophisticated quant hedge funds suffered losses as their ML models were first underhedged, and then overcompensated. We implement a gradient-based approach for precisely stress-testing how a trading model's forecasts can be manipulated, and their effects on downstream tasks at the trading execution level. We construct inputs -- whether in changes to sentiment or market variables -- that efficiently affect changes in the return distribution. In an industry-standard trading pipeline, we perturb model inputs for eight S&P 500 stocks. We find our approach discovers seemingly in-sample input settings that result in large negative shifts in return distributions. We provide the financial community with mechanisms to interpret ML forecasts in trading systems. For the security community, we provide a compelling application where studying ML robustness necessitates that one capture an end-to-end system's performance rather than study a ML model in isolation. Indeed, we show in our evaluation that errors in the forecasting model's predictions alone are not sufficient for trading decisions made based on these forecasts to yield a negative return.

Joint Shapley values: a measure of joint feature importance

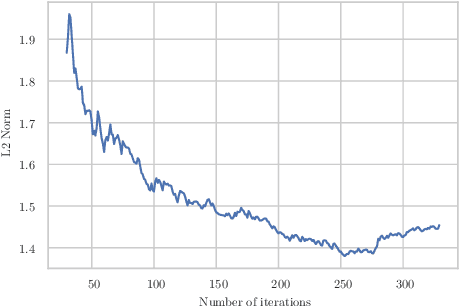
The Shapley value is one of the most widely used model-agnostic measures of feature importance in explainable AI: it has clear axiomatic foundations, is guaranteed to uniquely exist, and has a clear interpretation as a feature's average effect on a model's prediction. We introduce joint Shapley values, which directly extend the Shapley axioms. This preserves the classic Shapley value's intuitions: joint Shapley values measure a set of features' average effect on a model's prediction. We prove the uniqueness of joint Shapley values, for any order of explanation. Results for games show that joint Shapley values present different insights from existing interaction indices, which assess the effect of a feature within a set of features. Deriving joint Shapley values in ML attribution problems thus gives us the first measure of the joint effect of sets of features on model predictions. In a dataset with binary features, we present a presence-adjusted method for calculating global values that retains the efficiency property.

Asymmetric Shapley values: incorporating causal knowledge into model-agnostic explainability

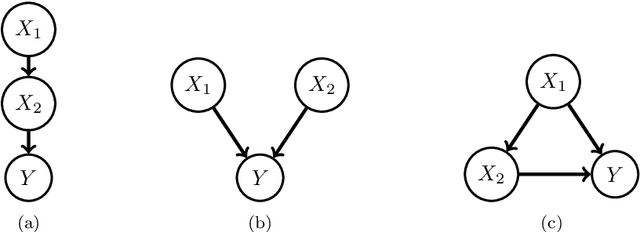
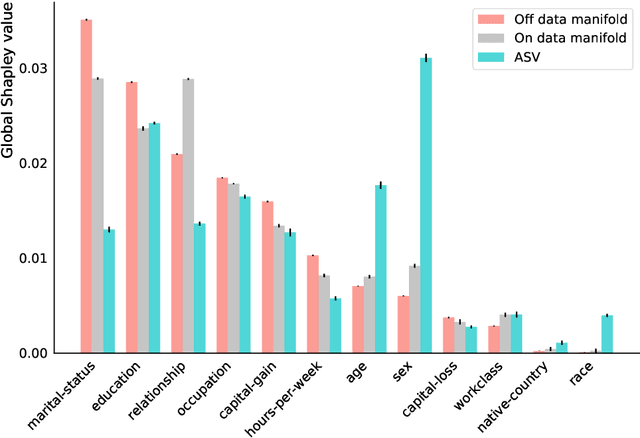
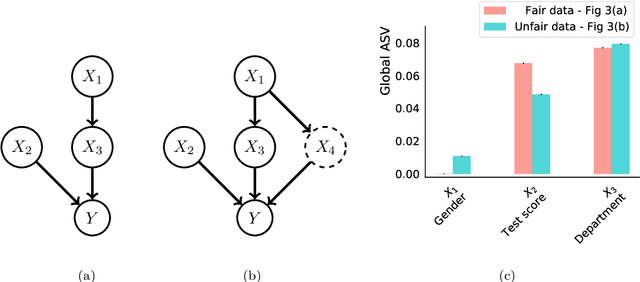
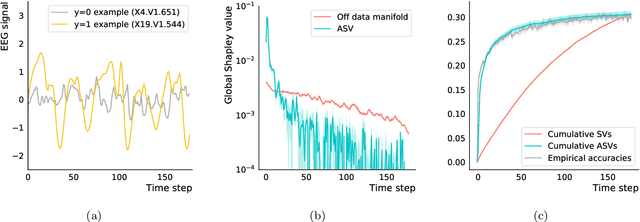
Explaining AI systems is fundamental both to the development of high performing models and to the trust placed in them by their users. A general framework for explaining any AI model is provided by the Shapley values that attribute the prediction output to the various model inputs ("features") in a principled and model-agnostic way. The outstanding strength of Shapley values is their combined generality and rigorous foundation: they can be used to explain any AI system, and one always understands their values as the unique attribution method satisfying a set of mathematical axioms. However, as a framework, Shapley values are too restrictive in one significant regard: they ignore all causal structure in the data. We introduce a less-restrictive framework for model-agnostic explainability: "Asymmetric" Shapley values. Asymmetric Shapley values (ASVs) are rigorously founded on a set of axioms, applicable to any AI system, and can flexibly incorporate any causal knowledge known a-priori to be respected by the data. We show through explicit, realistic examples that the ASV framework can be used to (i) improve model explanations by incorporating causal information, (ii) provide an unambiguous test for unfair discrimination based on simple policy articulations, (iii) enable sequentially incremental explanations in time-series models, and (iv) support feature-selection studies without the need for model retraining.