Enhancing Preference-based Linear Bandits via Human Response Time

Binary human choice feedback is widely used in interactive preference learning for its simplicity, but it provides limited information about preference strength. To overcome this limitation, we leverage human response times, which inversely correlate with preference strength, as complementary information. Our work integrates the EZ-diffusion model, which jointly models human choices and response times, into preference-based linear bandits. We introduce a computationally efficient utility estimator that reformulates the utility estimation problem using both choices and response times as a linear regression problem. Theoretical and empirical comparisons with traditional choice-only estimators reveal that for queries with strong preferences ("easy" queries), choices alone provide limited information, while response times offer valuable complementary information about preference strength. As a result, incorporating response times makes easy queries more useful. We demonstrate this advantage in the fixed-budget best-arm identification problem, with simulations based on three real-world datasets, consistently showing accelerated learning when response times are incorporated.

Ensuring Progress for Multiple Mobile Robots via Space Partitioning, Motion Rules, and Adaptively Centralized Conflict Resolution

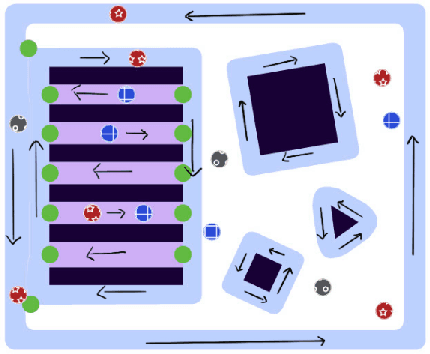
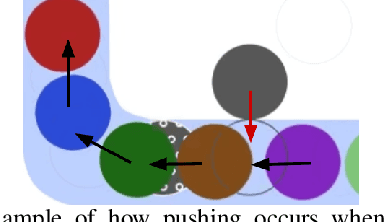
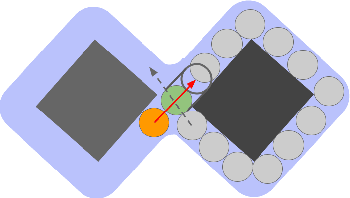
In environments where multiple robots must coordinate in a shared space, decentralized approaches allow for decoupled planning at the cost of global guarantees, while centralized approaches make the opposite trade-off. These solutions make a range of assumptions - commonly, that all the robots share the same planning strategies. In this work, we present a framework that ensures progress for all robots without assumptions on any robot's planning strategy by (1) generating a partition of the environment into "flow", "open", and "passage" regions and (2) imposing a set of rules for robot motion in these regions. These rules for robot motion prevent deadlock through an adaptively centralized protocol for resolving spatial conflicts between robots. Our proposed framework ensures progress for all robots without a grid-like discretization of the environment or strong requirements on robot communication, coordination, or cooperation. Each robot can freely choose how to plan and coordinate for itself, without being vulnerable to other robots or groups of robots blocking them from their goals, as long as they follow the rules when necessary. We describe our space partition and motion rules, prove that the motion rules suffice to guarantee progress in partitioned environments, and demonstrate several cases in simulated polygonal environments. This work strikes a balance between each robot's planning independence and a guarantee that each robot can always reach any goal in finite time.