A New Branch-and-Bound Pruning Framework for $\ell_0$-Regularized Problems

We consider the resolution of learning problems involving $\ell_0$-regularization via Branch-and-Bound (BnB) algorithms. These methods explore regions of the feasible space of the problem and check whether they do not contain solutions through "pruning tests". In standard implementations, evaluating a pruning test requires to solve a convex optimization problem, which may result in computational bottlenecks. In this paper, we present an alternative to implement pruning tests for some generic family of $\ell_0$-regularized problems. Our proposed procedure allows the simultaneous assessment of several regions and can be embedded in standard BnB implementations with a negligible computational overhead. We show through numerical simulations that our pruning strategy can improve the solving time of BnB procedures by several orders of magnitude for typical problems encountered in machine-learning applications.

One to beat them all: "RYU'' -- a unifying framework for the construction of safe balls

In this paper, we put forth a novel framework (named ``RYU'') for the construction of ``safe'' balls, i.e. regions that provably contain the dual solution of a target optimization problem. We concentrate on the standard setup where the cost function is the sum of two terms: a closed, proper, convex Lipschitz-smooth function and a closed, proper, convex function. The RYU framework is shown to generalize or improve upon all the results proposed in the last decade for the considered family of optimization problems.

Safe peeling for l0-regularized least-squares with supplementary material

We introduce a new methodology dubbed ``safe peeling'' to accelerate the resolution of L0-regularized least-squares problems via a Branch-and-Bound (BnB) algorithm. Our procedure enables to tighten the convex relaxation considered at each node of the BnB decision tree and therefore potentially allows for more aggressive pruning. Numerical simulations show that our proposed methodology leads to significant gains in terms of number of nodes explored and overall solving time.s show that our proposed methodology leads to significant gains in terms of number of nodes explored and overall solving time.

Beyond GAP screening for Lasso by exploiting new dual cutting half-spaces with supplementary material

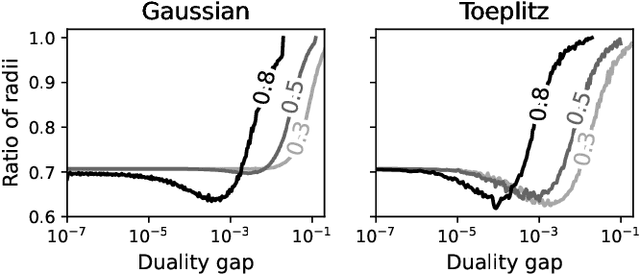
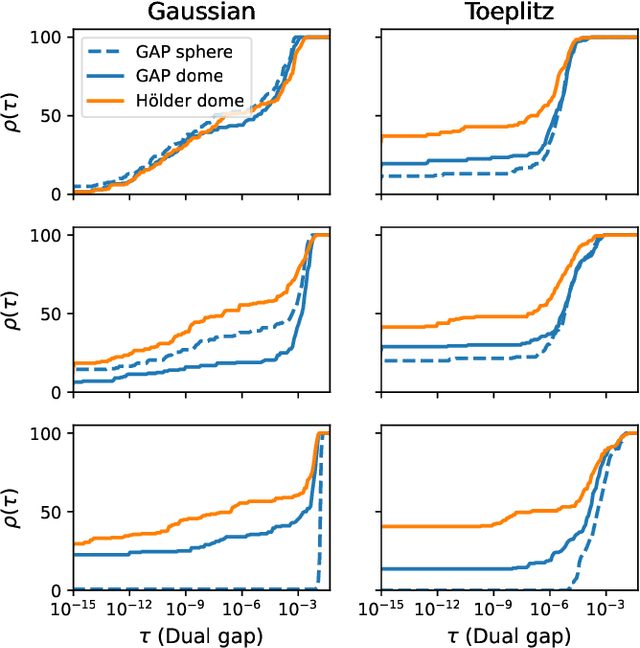
In this paper, we propose a novel safe screening test for Lasso. Our procedure is based on a safe region with a dome geometry and exploits a canonical representation of the set of half-spaces (referred to as "dual cutting half-spaces" in this paper) containing the dual feasible set. The proposed safe region is shown to be always included in the state-of-the-art "GAP Sphere" and "GAP Dome" proposed by Fercoq et al. (and strictly so under very mild conditions) while involving the same computational burden. Numerical experiments confirm that our new dome enables to devise more powerful screening tests than GAP regions and lead to significant acceleration to solve Lasso.

Safe rules for the identification of zeros in the solutions of the SLOPE problem

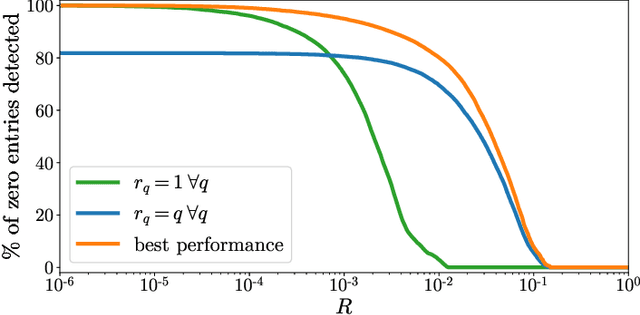
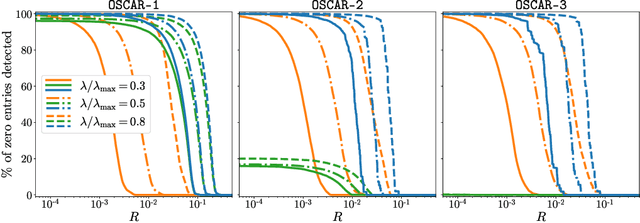
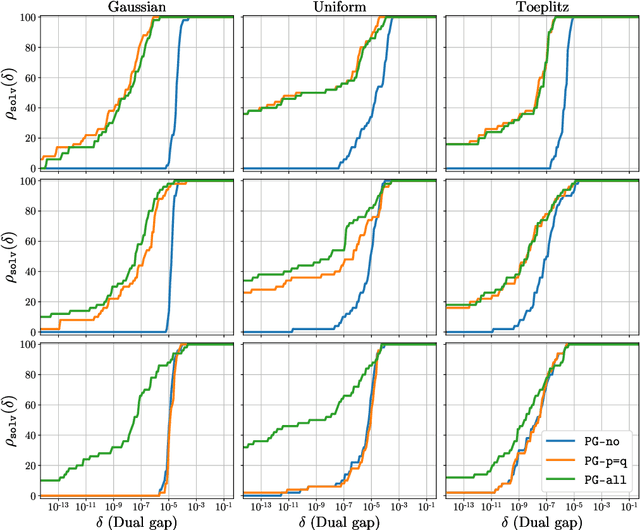
In this paper we propose a methodology to accelerate the resolution of the so-called ``Sorted L-One Penalized Estimation'' (SLOPE) problem. Our method leverages the concept of ``safe screening'', well-studied in the literature for \textit{group-separable} sparsity-inducing norms, and aims at identifying the zeros in the solution of SLOPE. More specifically, we introduce a family of \(n!\) safe screening rules for this problem, where \(n\) is the dimension of the primal variable, and propose a tractable procedure to verify if one of these tests is passed. Our procedure has a complexity \(\mathcal{O}(n\log n + LT)\) where \(T\leq n\) is a problem-dependent constant and \(L\) is the number of zeros identified by the tests. We assess the performance of our proposed method on a numerical benchmark and emphasize that it leads to significant computational savings in many setups.

Node-screening tests for L0-penalized least-squares problem with supplementary material

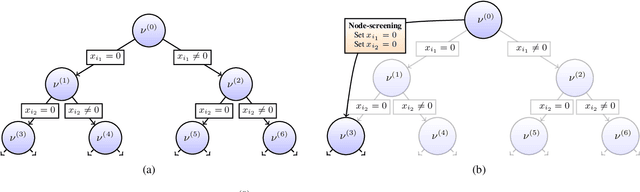
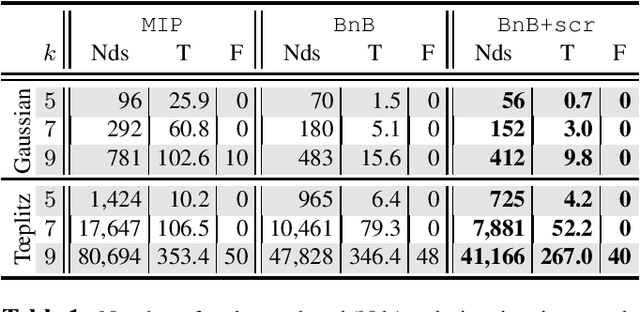
We present a novel screening methodology to safely discard irrelevant nodes within a generic branch-and-bound (BnB) algorithm solving the \(\ell_0\)-penalized least-squares problem. Our contribution is a set of two simple tests to detect sets of feasible vectors that cannot yield optimal solutions. This allows to prune nodes of the BnB exploration tree, thus reducing the overall solution time. One cornerstone of our contribution is a nesting property between tests at different nodes that allows to implement screening at low computational cost. Our work leverages the concept of safe screening, well known for sparsity-inducing convex problems, and some recent advances in this field for \(\ell_0\)-penalized regression problems.

Safe squeezing for antisparse coding

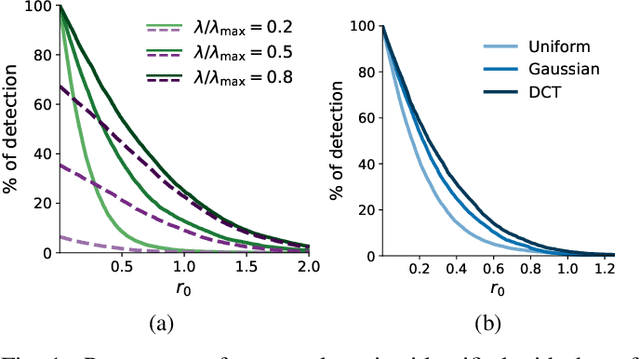
Spreading the information over all coefficients of a representation is a desirable property in many applications such as digital communication or machine learning. This so-called antisparse representation can be obtained by solving a convex program involving an $\ell_\infty$-norm penalty combined with a quadratic discrepancy. In this paper, we propose a new methodology, dubbed safe squeezing, to accelerate the computation of antisparse representation. We describe a test that allows to detect saturated entries in the solution of the optimization problem. The contribution of these entries is compacted into a single vector, thus operating a form of dimensionality reduction. We propose two algorithms to solve the resulting lower dimensional problem. Numerical experiments show the effectiveness of the proposed method to detect the saturated components of the solution and illustrates the induced computational gains in the resolution of the antisparse problem.

Bayesian nonparametric Principal Component Analysis

Principal component analysis (PCA) is very popular to perform dimension reduction. The selection of the number of significant components is essential but often based on some practical heuristics depending on the application. Only few works have proposed a probabilistic approach able to infer the number of significant components. To this purpose, this paper introduces a Bayesian nonparametric principal component analysis (BNP-PCA). The proposed model projects observations onto a random orthogonal basis which is assigned a prior distribution defined on the Stiefel manifold. The prior on factor scores involves an Indian buffet process to model the uncertainty related to the number of components. The parameters of interest as well as the nuisance parameters are finally inferred within a fully Bayesian framework via Monte Carlo sampling. A study of the (in-)consistence of the marginal maximum a posteriori estimator of the latent dimension is carried out. A new estimator of the subspace dimension is proposed. Moreover, for sake of statistical significance, a Kolmogorov-Smirnov test based on the posterior distribution of the principal components is used to refine this estimate. The behaviour of the algorithm is first studied on various synthetic examples. Finally, the proposed BNP dimension reduction approach is shown to be easily yet efficiently coupled with clustering or latent factor models within a unique framework.

Bayesian anti-sparse coding

Sparse representations have proven their efficiency in solving a wide class of inverse problems encountered in signal and image processing. Conversely, enforcing the information to be spread uniformly over representation coefficients exhibits relevant properties in various applications such as digital communications. Anti-sparse regularization can be naturally expressed through an $\ell_{\infty}$-norm penalty. This paper derives a probabilistic formulation of such representations. A new probability distribution, referred to as the democratic prior, is first introduced. Its main properties as well as three random variate generators for this distribution are derived. Then this probability distribution is used as a prior to promote anti-sparsity in a Gaussian linear inverse problem, yielding a fully Bayesian formulation of anti-sparse coding. Two Markov chain Monte Carlo (MCMC) algorithms are proposed to generate samples according to the posterior distribution. The first one is a standard Gibbs sampler. The second one uses Metropolis-Hastings moves that exploit the proximity mapping of the log-posterior distribution. These samples are used to approximate maximum a posteriori and minimum mean square error estimators of both parameters and hyperparameters. Simulations on synthetic data illustrate the performances of the two proposed samplers, for both complete and over-complete dictionaries. All results are compared to the recent deterministic variational FITRA algorithm.