Hong-Phuong Dang
One to beat them all: "RYU'' -- a unifying framework for the construction of safe balls
Dec 01, 2023Abstract:In this paper, we put forth a novel framework (named ``RYU'') for the construction of ``safe'' balls, i.e. regions that provably contain the dual solution of a target optimization problem. We concentrate on the standard setup where the cost function is the sum of two terms: a closed, proper, convex Lipschitz-smooth function and a closed, proper, convex function. The RYU framework is shown to generalize or improve upon all the results proposed in the last decade for the considered family of optimization problems.
Beyond GAP screening for Lasso by exploiting new dual cutting half-spaces with supplementary material
Mar 02, 2022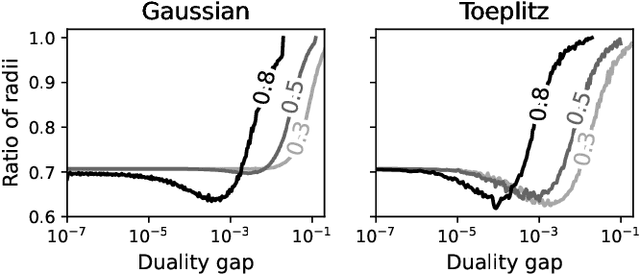
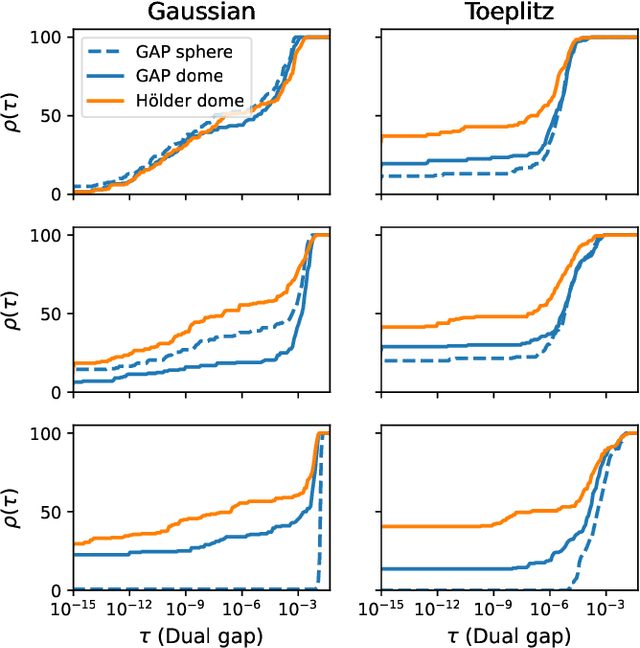
Abstract:In this paper, we propose a novel safe screening test for Lasso. Our procedure is based on a safe region with a dome geometry and exploits a canonical representation of the set of half-spaces (referred to as "dual cutting half-spaces" in this paper) containing the dual feasible set. The proposed safe region is shown to be always included in the state-of-the-art "GAP Sphere" and "GAP Dome" proposed by Fercoq et al. (and strictly so under very mild conditions) while involving the same computational burden. Numerical experiments confirm that our new dome enables to devise more powerful screening tests than GAP regions and lead to significant acceleration to solve Lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge