Safe squeezing for antisparse coding
Paper and Code
Nov 18, 2019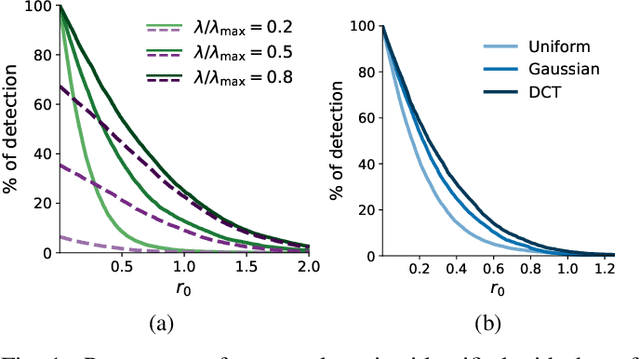
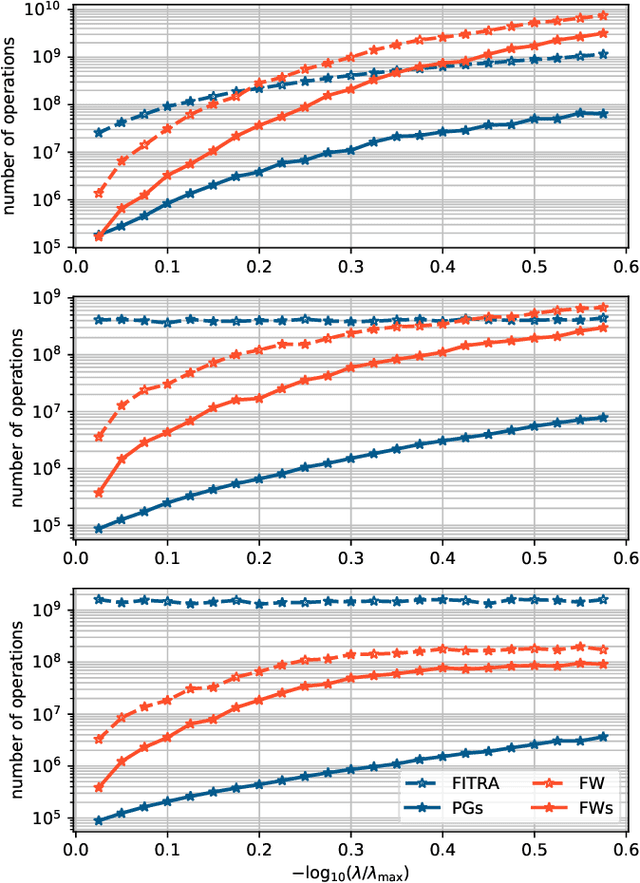
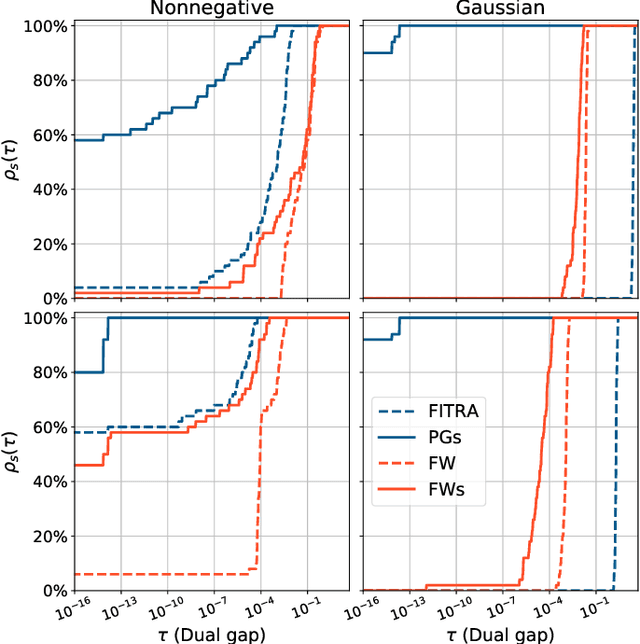
Spreading the information over all coefficients of a representation is a desirable property in many applications such as digital communication or machine learning. This so-called antisparse representation can be obtained by solving a convex program involving an $\ell_\infty$-norm penalty combined with a quadratic discrepancy. In this paper, we propose a new methodology, dubbed safe squeezing, to accelerate the computation of antisparse representation. We describe a test that allows to detect saturated entries in the solution of the optimization problem. The contribution of these entries is compacted into a single vector, thus operating a form of dimensionality reduction. We propose two algorithms to solve the resulting lower dimensional problem. Numerical experiments show the effectiveness of the proposed method to detect the saturated components of the solution and illustrates the induced computational gains in the resolution of the antisparse problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge