A Generic Branch-and-Bound Algorithm for $\ell_0$-Penalized Problems with Supplementary Material

We present a generic Branch-and-Bound procedure designed to solve L0-penalized optimization problems. Existing approaches primarily focus on quadratic losses and construct relaxations using "Big-M" constraints and/or L2-norm penalties. In contrast, our method accommodates a broader class of loss functions and allows greater flexibility in relaxation design through a general penalty term, encompassing existing techniques as special cases. We establish theoretical results ensuring that all key quantities required for the Branch-and-Bound implementation admit closed-form expressions under the general blanket assumptions considered in our work. Leveraging this framework, we introduce El0ps, an open-source Python solver with a plug-and-play workflow that enables user-defined losses and penalties in L0-penalized problems. Through extensive numerical experiments, we demonstrate that El0ps achieves state-of-the-art performance on classical instances and extends computational feasibility to previously intractable ones.

El0ps: An Exact L0-regularized Problems Solver

This paper presents El0ps, a Python toolbox providing several utilities to handle L0-regularized problems related to applications in machine learning, statistics, and signal processing, among other fields. In contrast to existing toolboxes, El0ps allows users to define custom instances of these problems through a flexible framework, provides a dedicated solver achieving state-of-the-art performance, and offers several built-in machine learning pipelines. Our aim with El0ps is to provide a comprehensive tool which opens new perspectives for the integration of L0-regularized problems in practical applications.

Safe peeling for l0-regularized least-squares with supplementary material

We introduce a new methodology dubbed ``safe peeling'' to accelerate the resolution of L0-regularized least-squares problems via a Branch-and-Bound (BnB) algorithm. Our procedure enables to tighten the convex relaxation considered at each node of the BnB decision tree and therefore potentially allows for more aggressive pruning. Numerical simulations show that our proposed methodology leads to significant gains in terms of number of nodes explored and overall solving time.s show that our proposed methodology leads to significant gains in terms of number of nodes explored and overall solving time.

Node-screening tests for L0-penalized least-squares problem with supplementary material

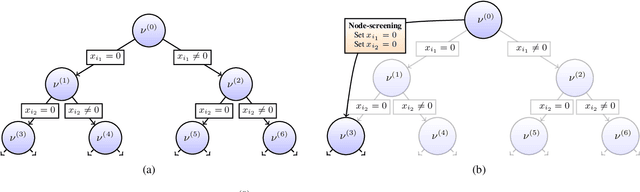
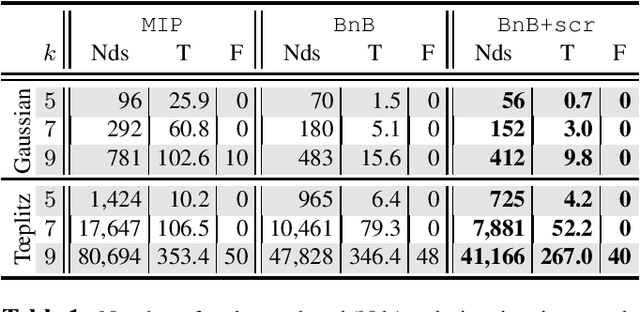
We present a novel screening methodology to safely discard irrelevant nodes within a generic branch-and-bound (BnB) algorithm solving the \(\ell_0\)-penalized least-squares problem. Our contribution is a set of two simple tests to detect sets of feasible vectors that cannot yield optimal solutions. This allows to prune nodes of the BnB exploration tree, thus reducing the overall solution time. One cornerstone of our contribution is a nesting property between tests at different nodes that allows to implement screening at low computational cost. Our work leverages the concept of safe screening, well known for sparsity-inducing convex problems, and some recent advances in this field for \(\ell_0\)-penalized regression problems.