Node-screening tests for L0-penalized least-squares problem with supplementary material

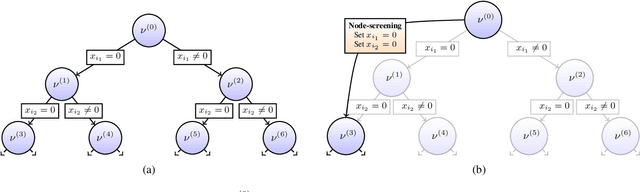
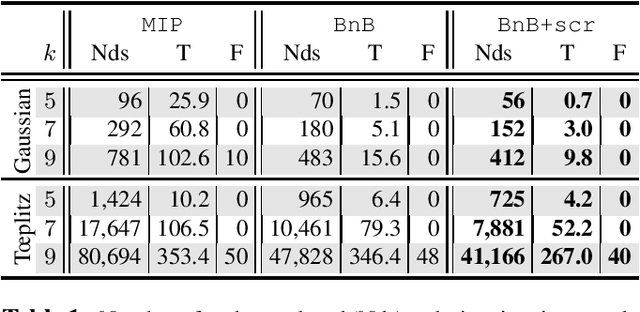
We present a novel screening methodology to safely discard irrelevant nodes within a generic branch-and-bound (BnB) algorithm solving the \(\ell_0\)-penalized least-squares problem. Our contribution is a set of two simple tests to detect sets of feasible vectors that cannot yield optimal solutions. This allows to prune nodes of the BnB exploration tree, thus reducing the overall solution time. One cornerstone of our contribution is a nesting property between tests at different nodes that allows to implement screening at low computational cost. Our work leverages the concept of safe screening, well known for sparsity-inducing convex problems, and some recent advances in this field for \(\ell_0\)-penalized regression problems.