Safe rules for the identification of zeros in the solutions of the SLOPE problem
Paper and Code
Oct 22, 2021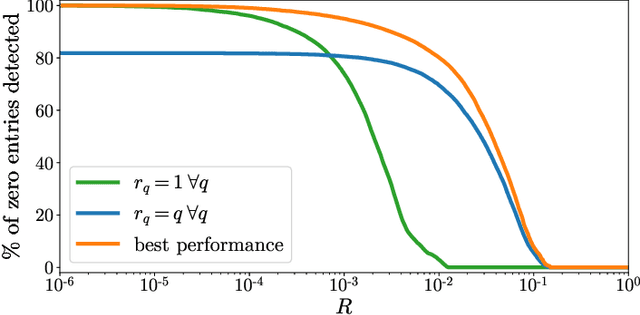
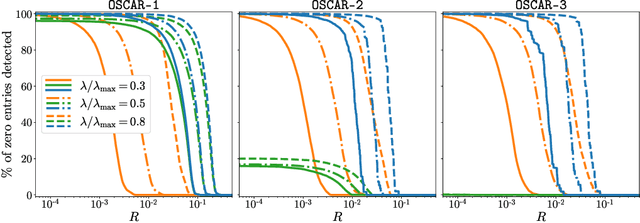
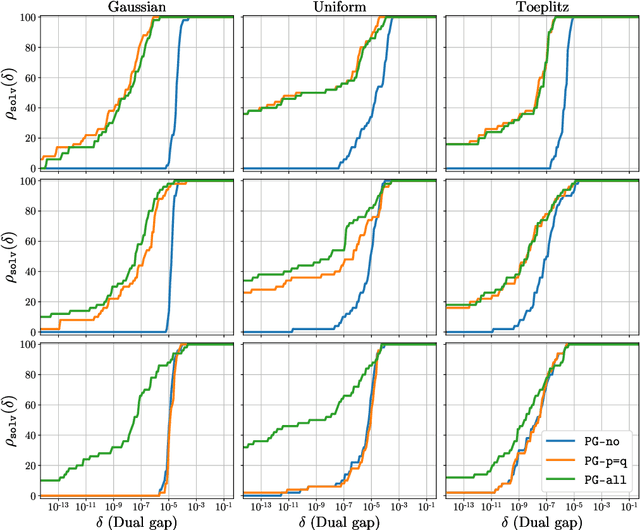
In this paper we propose a methodology to accelerate the resolution of the so-called ``Sorted L-One Penalized Estimation'' (SLOPE) problem. Our method leverages the concept of ``safe screening'', well-studied in the literature for \textit{group-separable} sparsity-inducing norms, and aims at identifying the zeros in the solution of SLOPE. More specifically, we introduce a family of \(n!\) safe screening rules for this problem, where \(n\) is the dimension of the primal variable, and propose a tractable procedure to verify if one of these tests is passed. Our procedure has a complexity \(\mathcal{O}(n\log n + LT)\) where \(T\leq n\) is a problem-dependent constant and \(L\) is the number of zeros identified by the tests. We assess the performance of our proposed method on a numerical benchmark and emphasize that it leads to significant computational savings in many setups.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge