Prototype-based Optimal Transport for Out-of-Distribution Detection

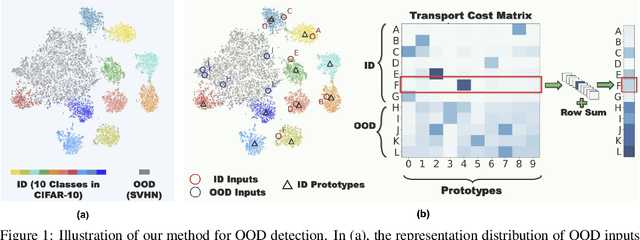
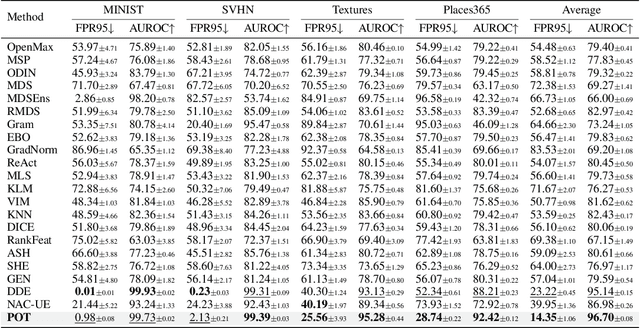
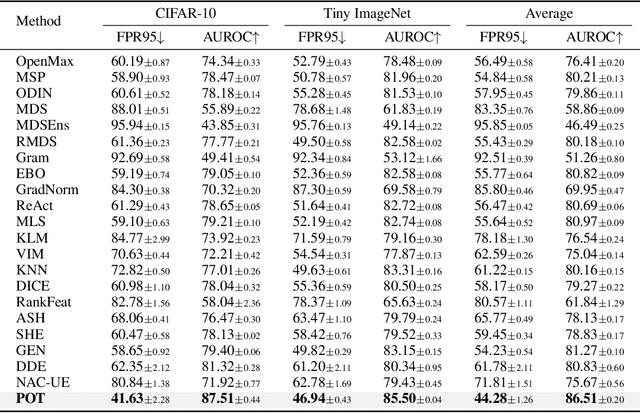
Detecting Out-of-Distribution (OOD) inputs is crucial for improving the reliability of deep neural networks in the real-world deployment. In this paper, inspired by the inherent distribution shift between ID and OOD data, we propose a novel method that leverages optimal transport to measure the distribution discrepancy between test inputs and ID prototypes. The resulting transport costs are used to quantify the individual contribution of each test input to the overall discrepancy, serving as a desirable measure for OOD detection. To address the issue that solely relying on the transport costs to ID prototypes is inadequate for identifying OOD inputs closer to ID data, we generate virtual outliers to approximate the OOD region via linear extrapolation. By combining the transport costs to ID prototypes with the costs to virtual outliers, the detection of OOD data near ID data is emphasized, thereby enhancing the distinction between ID and OOD inputs. Experiments demonstrate the superiority of our method over state-of-the-art methods.

Detecting Out-of-Distribution Samples via Conditional Distribution Entropy with Optimal Transport

When deploying a trained machine learning model in the real world, it is inevitable to receive inputs from out-of-distribution (OOD) sources. For instance, in continual learning settings, it is common to encounter OOD samples due to the non-stationarity of a domain. More generally, when we have access to a set of test inputs, the existing rich line of OOD detection solutions, especially the recent promise of distance-based methods, falls short in effectively utilizing the distribution information from training samples and test inputs. In this paper, we argue that empirical probability distributions that incorporate geometric information from both training samples and test inputs can be highly beneficial for OOD detection in the presence of test inputs available. To address this, we propose to model OOD detection as a discrete optimal transport problem. Within the framework of optimal transport, we propose a novel score function known as the \emph{conditional distribution entropy} to quantify the uncertainty of a test input being an OOD sample. Our proposal inherits the merits of certain distance-based methods while eliminating the reliance on distribution assumptions, a-prior knowledge, and specific training mechanisms. Extensive experiments conducted on benchmark datasets demonstrate that our method outperforms its competitors in OOD detection.