Feedback-Enhanced Online Multiple Testing with Applications to Conformal Selection

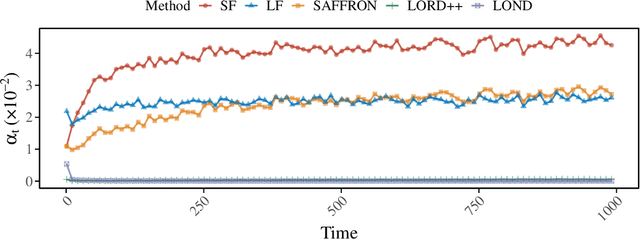
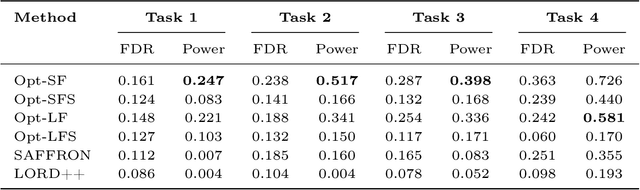
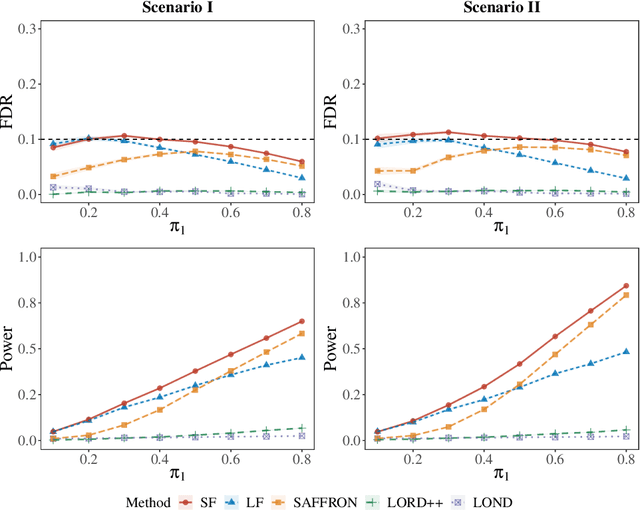
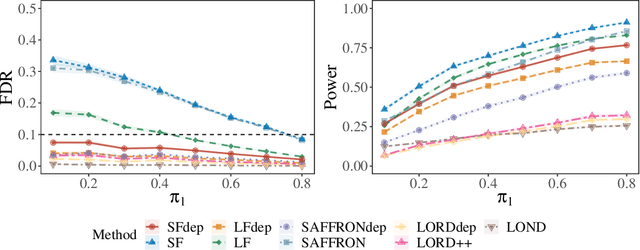
We study online multiple testing with feedback, where decisions are made sequentially and the true state of the hypothesis is revealed after the decision has been made, either instantly or with a delay. We propose GAIF, a feedback-enhanced generalized alpha-investing framework that dynamically adjusts thresholds using revealed outcomes, ensuring finite-sample false discovery rate (FDR)/marginal FDR control. Extending GAIF to online conformal testing, we construct independent conformal $p$-values and introduce a feedback-driven model selection criterion to identify the best model/score, thereby improving statistical power. We demonstrate the effectiveness of our methods through numerical simulations and real-data applications.

Conformal Prediction with Cellwise Outliers: A Detect-then-Impute Approach

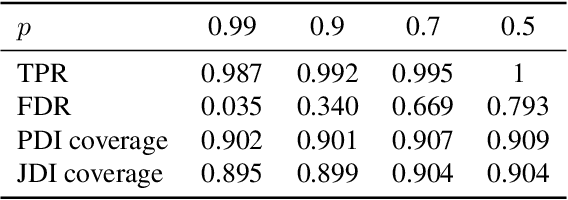
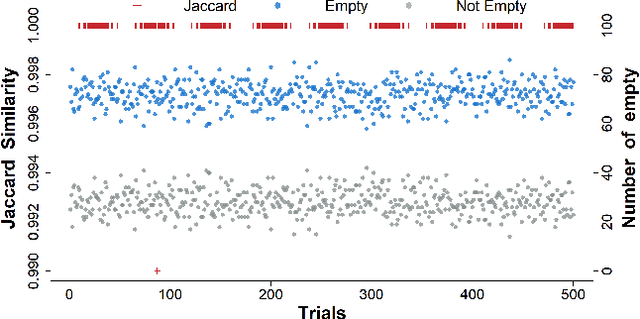
Conformal prediction is a powerful tool for constructing prediction intervals for black-box models, providing a finite sample coverage guarantee for exchangeable data. However, this exchangeability is compromised when some entries of the test feature are contaminated, such as in the case of cellwise outliers. To address this issue, this paper introduces a novel framework called detect-then-impute conformal prediction. This framework first employs an outlier detection procedure on the test feature and then utilizes an imputation method to fill in those cells identified as outliers. To quantify the uncertainty in the processed test feature, we adaptively apply the detection and imputation procedures to the calibration set, thereby constructing exchangeable features for the conformal prediction interval of the test label. We develop two practical algorithms, PDI-CP and JDI-CP, and provide a distribution-free coverage analysis under some commonly used detection and imputation procedures. Notably, JDI-CP achieves a finite sample $1-2\alpha$ coverage guarantee. Numerical experiments on both synthetic and real datasets demonstrate that our proposed algorithms exhibit robust coverage properties and comparable efficiency to the oracle baseline.

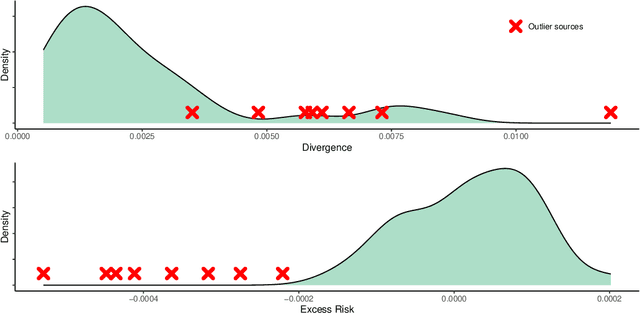
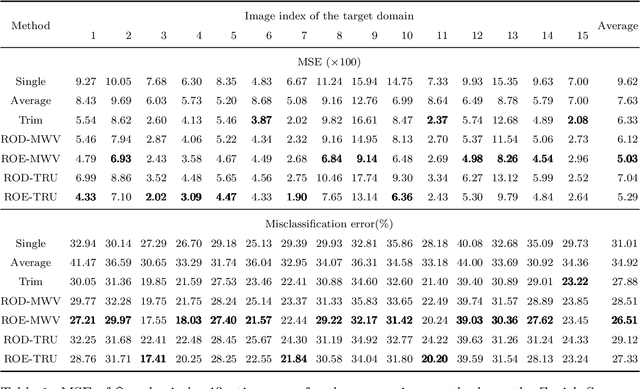
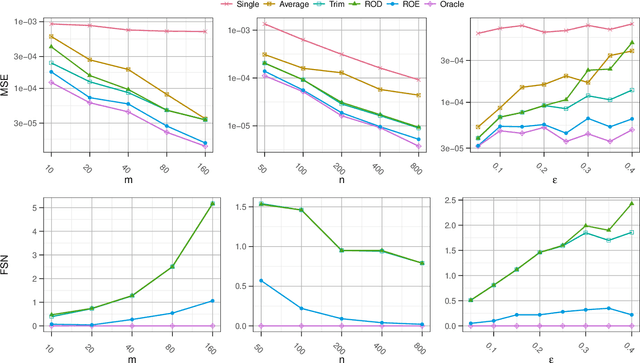
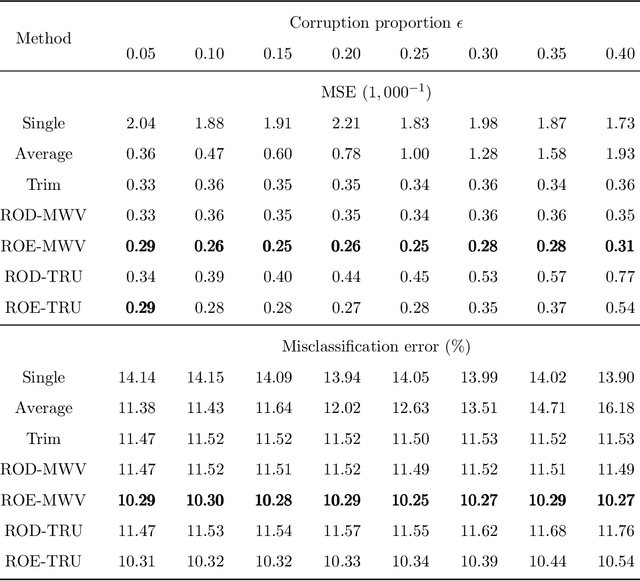
Robust Multi-Source Domain Adaptation under Label Shift

As the volume of data continues to expand, it becomes increasingly common for data to be aggregated from multiple sources. Leveraging multiple sources for model training typically achieves better predictive performance on test datasets. Unsupervised multi-source domain adaptation aims to predict labels of unlabeled samples in the target domain by using labeled samples from source domains. This work focuses on robust multi-source domain adaptation for multi-category classification problems against the heterogeneity of label shift and data contamination. We investigate a domain-weighted empirical risk minimization framework for robust estimation of the target domain's class proportion. Inspired by outlier detection techniques, we propose a refinement procedure within this framework. With the estimated class proportion, robust classifiers for the target domain can be constructed. Theoretically, we study the finite-sample error bounds of the domain-weighted empirical risk minimization and highlight the improvement of the refinement step. Numerical simulations and real-data applications demonstrate the superiority of the proposed method.

Error-quantified Conformal Inference for Time Series

Uncertainty quantification in time series prediction is challenging due to the temporal dependence and distribution shift on sequential data. Conformal inference provides a pivotal and flexible instrument for assessing the uncertainty of machine learning models through prediction sets. Recently, a series of online conformal inference methods updated thresholds of prediction sets by performing online gradient descent on a sequence of quantile loss functions. A drawback of such methods is that they only use the information of revealed non-conformity scores via miscoverage indicators but ignore error quantification, namely the distance between the non-conformity score and the current threshold. To accurately leverage the dynamic of miscoverage error, we propose \textit{Error-quantified Conformal Inference} (ECI) by smoothing the quantile loss function. ECI introduces a continuous and adaptive feedback scale with the miscoverage error, rather than simple binary feedback in existing methods. We establish a long-term coverage guarantee for ECI under arbitrary dependence and distribution shift. The extensive experimental results show that ECI can achieve valid miscoverage control and output tighter prediction sets than other baselines.

Conditional Testing based on Localized Conformal p-values

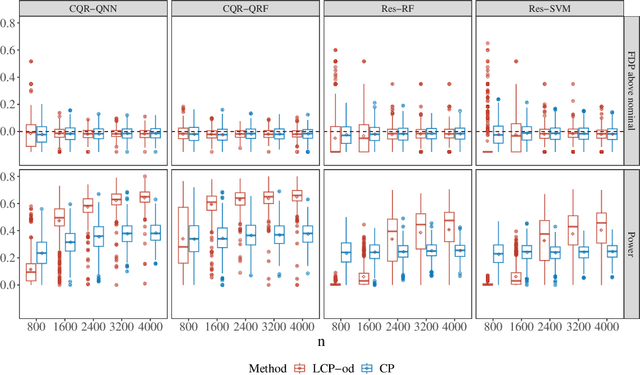
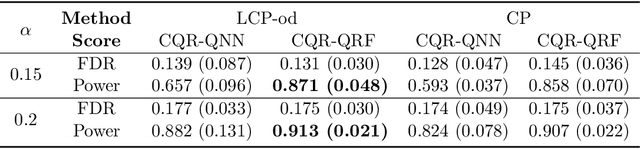
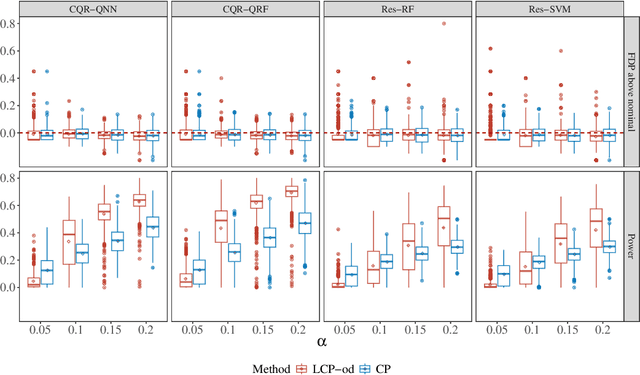
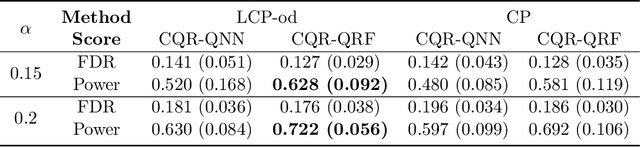
In this paper, we address conditional testing problems through the conformal inference framework. We define the localized conformal p-values by inverting prediction intervals and prove their theoretical properties. These defined p-values are then applied to several conditional testing problems to illustrate their practicality. Firstly, we propose a conditional outlier detection procedure to test for outliers in the conditional distribution with finite-sample false discovery rate (FDR) control. We also introduce a novel conditional label screening problem with the goal of screening multivariate response variables and propose a screening procedure to control the family-wise error rate (FWER). Finally, we consider the two-sample conditional distribution test and define a weighted U-statistic through the aggregation of localized p-values. Numerical simulations and real-data examples validate the superior performance of our proposed strategies.

CAS: A General Algorithm for Online Selective Conformal Prediction with FCR Control

We study the problem of post-selection predictive inference in an online fashion. To avoid devoting resources to unimportant units, a preliminary selection of the current individual before reporting its prediction interval is common and meaningful in online predictive tasks. Since the online selection causes a temporal multiplicity in the selected prediction intervals, it is important to control the real-time false coverage-statement rate (FCR) to measure the averaged miscoverage error. We develop a general framework named CAS (Calibration after Adaptive Selection) that can wrap around any prediction model and online selection rule to output post-selection prediction intervals. If the current individual is selected, we first perform an adaptive selection on historical data to construct a calibration set, then output a conformal prediction interval for the unobserved label. We provide tractable constructions for the calibration set for popular online selection rules. We proved that CAS can achieve an exact selection-conditional coverage guarantee in the finite-sample and distribution-free regimes. For the decision-driven selection rule, including most online multiple-testing procedures, CAS can exactly control the real-time FCR below the target level without any distributional assumptions. For the online selection with symmetric thresholds, we establish the error bound for the control gap of FCR under mild distributional assumptions. To account for the distribution shift in online data, we also embed CAS into some recent dynamic conformal prediction methods and examine the long-run FCR control. Numerical results on both synthetic and real data corroborate that CAS can effectively control FCR around the target level and yield more narrowed prediction intervals over existing baselines across various settings.