Disentangled Hyperbolic Representation Learning for Heterogeneous Graphs

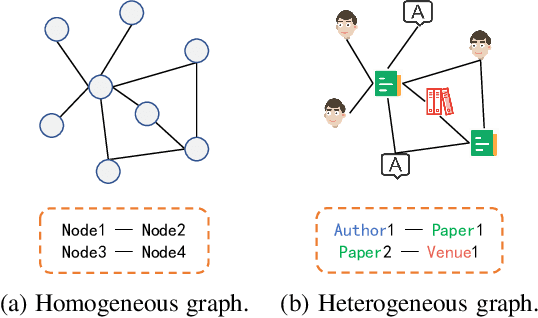
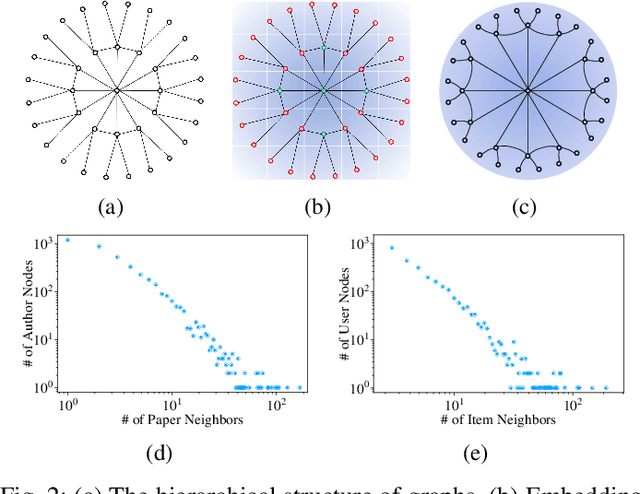
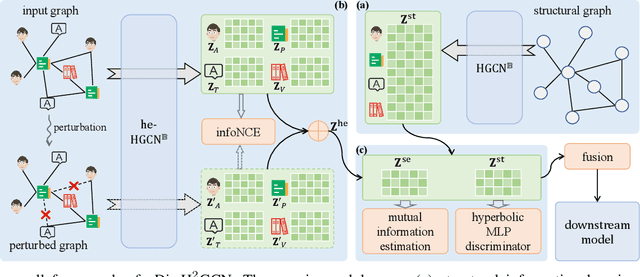
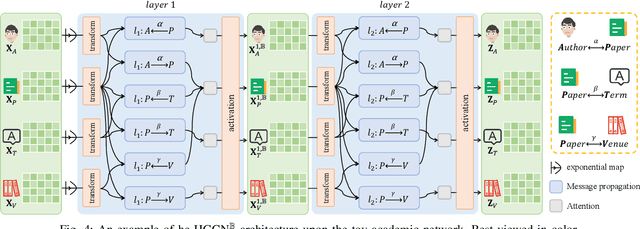
Heterogeneous graphs have attracted a lot of research interests recently due to the success for representing complex real-world systems. However, existing methods have two pain points in embedding them into low-dimensional spaces: the mixing of structural and semantic information, and the distributional mismatch between data and embedding spaces. These two challenges require representation methods to consider the global and partial data distributions while unmixing the information. Therefore, in this paper, we propose $\text{Dis-H}^2\text{GCN}$, a Disentangled Hyperbolic Heterogeneous Graph Convolutional Network. On the one hand, we leverage the mutual information minimization and discrimination maximization constraints to disentangle the semantic features from comprehensively learned representations by independent message propagation for each edge type, away from the pure structural features. On the other hand, the entire model is constructed upon the hyperbolic geometry to narrow the gap between data distributions and representing spaces. We evaluate our proposed $\text{Dis-H}^2\text{GCN}$ on five real-world heterogeneous graph datasets across two downstream tasks: node classification and link prediction. The results demonstrate its superiority over state-of-the-art methods, showcasing the effectiveness of our method in disentangling and representing heterogeneous graph data in hyperbolic spaces.

HGWaveNet: A Hyperbolic Graph Neural Network for Temporal Link Prediction

Temporal link prediction, aiming to predict future edges between paired nodes in a dynamic graph, is of vital importance in diverse applications. However, existing methods are mainly built upon uniform Euclidean space, which has been found to be conflict with the power-law distributions of real-world graphs and unable to represent the hierarchical connections between nodes effectively. With respect to the special data characteristic, hyperbolic geometry offers an ideal alternative due to its exponential expansion property. In this paper, we propose HGWaveNet, a novel hyperbolic graph neural network that fully exploits the fitness between hyperbolic spaces and data distributions for temporal link prediction. Specifically, we design two key modules to learn the spatial topological structures and temporal evolutionary information separately. On the one hand, a hyperbolic diffusion graph convolution (HDGC) module effectively aggregates information from a wider range of neighbors. On the other hand, the internal order of causal correlation between historical states is captured by hyperbolic dilated causal convolution (HDCC) modules. The whole model is built upon the hyperbolic spaces to preserve the hierarchical structural information in the entire data flow. To prove the superiority of HGWaveNet, extensive experiments are conducted on six real-world graph datasets and the results show a relative improvement by up to 6.67% on AUC for temporal link prediction over SOTA methods.

H2TNE: Temporal Heterogeneous Information Network Embedding in Hyperbolic Spaces

Temporal heterogeneous information network (temporal HIN) embedding, aiming to represent various types of nodes of different timestamps into low dimensional spaces while preserving structural and semantic information, is of vital importance in diverse real-life tasks. Researchers have made great efforts on temporal HIN embedding in Euclidean spaces and got some considerable achievements. However, there is always a fundamental conflict that many real-world networks show hierarchical property and power-law distribution, and are not isometric of Euclidean spaces. Recently, representation learning in hyperbolic spaces has been proved to be valid for data with hierarchical and power-law structure. Inspired by this character, we propose a hyperbolic heterogeneous temporal network embedding (H2TNE) model for temporal HINs. Specifically, we leverage a temporally and heterogeneously double-constrained random walk strategy to capture the structural and semantic information, and then calculate the embedding by exploiting hyperbolic distance in proximity measurement. Experimental results show that our method has superior performance on temporal link prediction and node classification compared with SOTA models.