Disentangled Hyperbolic Representation Learning for Heterogeneous Graphs
Paper and Code
Jun 14, 2024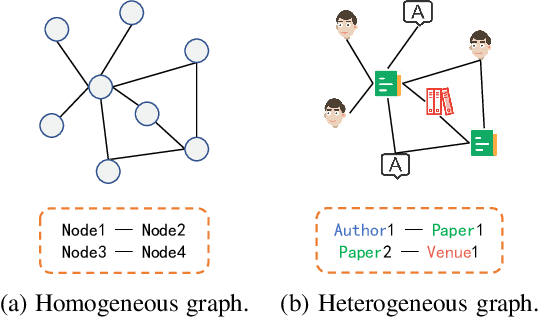
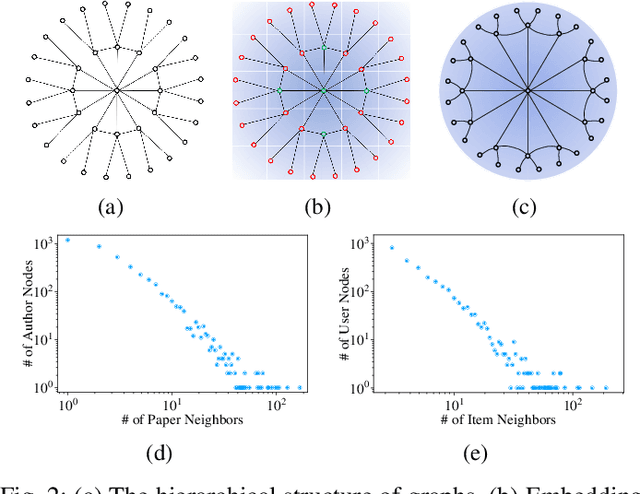
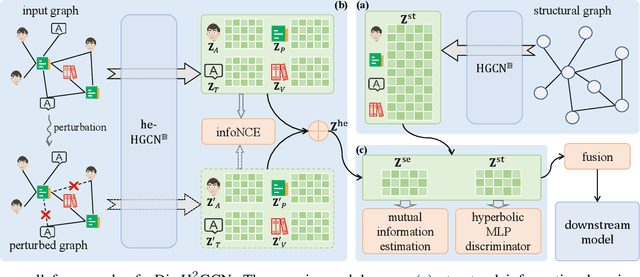
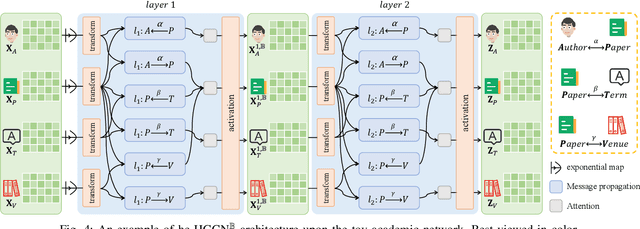
Heterogeneous graphs have attracted a lot of research interests recently due to the success for representing complex real-world systems. However, existing methods have two pain points in embedding them into low-dimensional spaces: the mixing of structural and semantic information, and the distributional mismatch between data and embedding spaces. These two challenges require representation methods to consider the global and partial data distributions while unmixing the information. Therefore, in this paper, we propose $\text{Dis-H}^2\text{GCN}$, a Disentangled Hyperbolic Heterogeneous Graph Convolutional Network. On the one hand, we leverage the mutual information minimization and discrimination maximization constraints to disentangle the semantic features from comprehensively learned representations by independent message propagation for each edge type, away from the pure structural features. On the other hand, the entire model is constructed upon the hyperbolic geometry to narrow the gap between data distributions and representing spaces. We evaluate our proposed $\text{Dis-H}^2\text{GCN}$ on five real-world heterogeneous graph datasets across two downstream tasks: node classification and link prediction. The results demonstrate its superiority over state-of-the-art methods, showcasing the effectiveness of our method in disentangling and representing heterogeneous graph data in hyperbolic spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge