Deep Diffusion Maps

One of the fundamental problems within the field of machine learning is dimensionality reduction. Dimensionality reduction methods make it possible to combat the so-called curse of dimensionality, visualize high-dimensional data and, in general, improve the efficiency of storing and processing large data sets. One of the best-known nonlinear dimensionality reduction methods is Diffusion Maps. However, despite their virtues, both Diffusion Maps and many other manifold learning methods based on the spectral decomposition of kernel matrices have drawbacks such as the inability to apply them to data outside the initial set, their computational complexity, and high memory costs for large data sets. In this work, we propose to alleviate these problems by resorting to deep learning. Specifically, a new formulation of Diffusion Maps embedding is offered as a solution to a certain unconstrained minimization problem and, based on it, a cost function to train a neural network which computes Diffusion Maps embedding -- both inside and outside the training sample -- without the need to perform any spectral decomposition. The capabilities of this approach are compared on different data sets, both real and synthetic, with those of Diffusion Maps and the Nystrom method.

Fault Detection in Induction Motors using Functional Dimensionality Reduction Methods

The implementation of strategies for fault detection and diagnosis on rotating electrical machines is crucial for the reliability and safety of modern industrial systems. The contribution of this work is a methodology that combines conventional strategy of Motor Current Signature Analysis with functional dimensionality reduction methods, namely Functional Principal Components Analysis and Functional Diffusion Maps, for detecting and classifying fault conditions in induction motors. The results obtained from the proposed scheme are very encouraging, revealing a potential use in the future not only for real-time detection of the presence of a fault in an induction motor, but also in the identification of a greater number of types of faults present through an offline analysis.

Robust Classification of Graph-Based Data

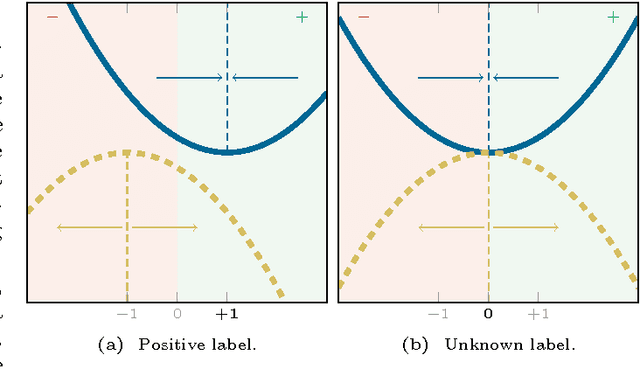
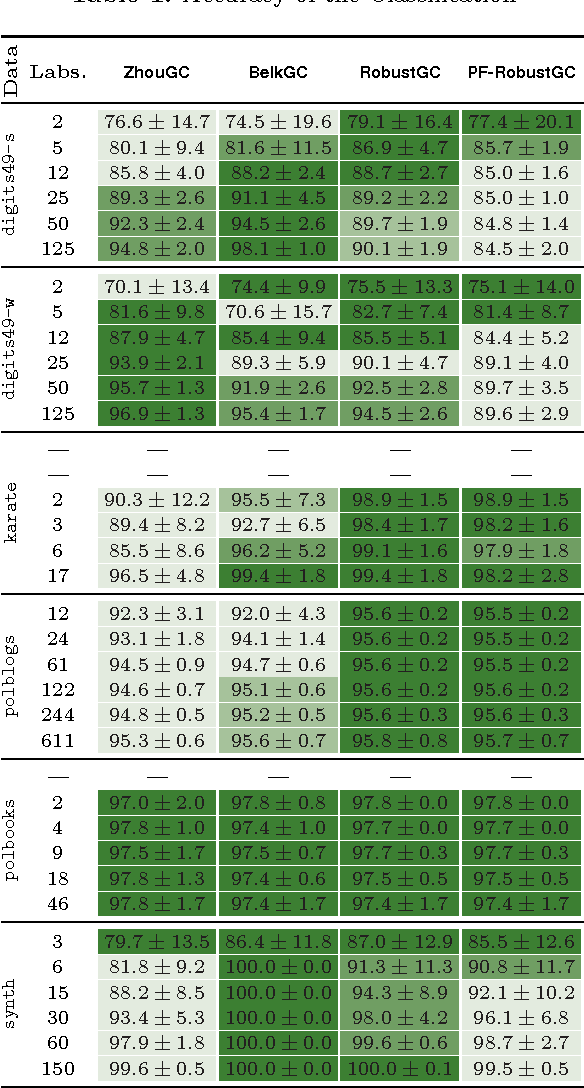
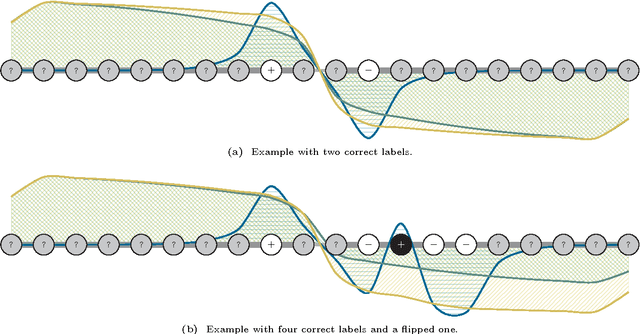
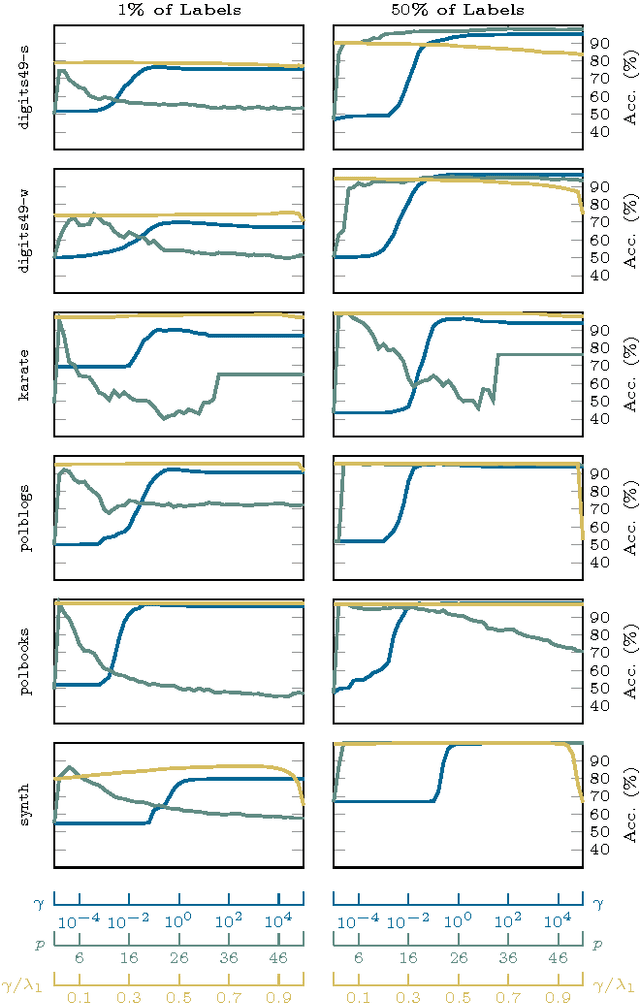
A graph-based classification method is proposed for semi-supervised learning in the case of Euclidean data and for classification in the case of graph data. Our manifold learning technique is based on a convex optimization problem involving a convex quadratic regularization term and a concave quadratic loss function with a trade-off parameter carefully chosen so that the objective function remains convex. As shown empirically, the advantage of considering a concave loss function is that the learning problem becomes more robust in the presence of noisy labels. Furthermore, the loss function considered here is then more similar to a classification loss while several other methods treat graph-based classification problems as regression problems.

Modified Frank-Wolfe Algorithm for Enhanced Sparsity in Support Vector Machine Classifiers

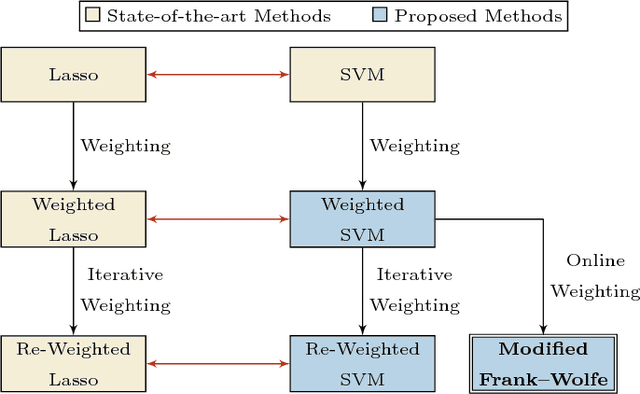
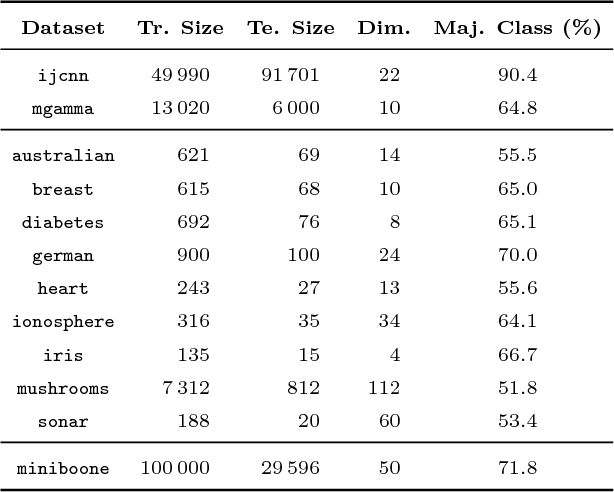
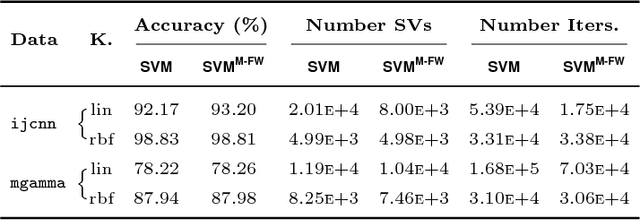
This work proposes a new algorithm for training a re-weighted L2 Support Vector Machine (SVM), inspired on the re-weighted Lasso algorithm of Cand\`es et al. and on the equivalence between Lasso and SVM shown recently by Jaggi. In particular, the margin required for each training vector is set independently, defining a new weighted SVM model. These weights are selected to be binary, and they are automatically adapted during the training of the model, resulting in a variation of the Frank-Wolfe optimization algorithm with essentially the same computational complexity as the original algorithm. As shown experimentally, this algorithm is computationally cheaper to apply since it requires less iterations to converge, and it produces models with a sparser representation in terms of support vectors and which are more stable with respect to the selection of the regularization hyper-parameter.

Convex Formulation for Kernel PCA and its Use in Semi-Supervised Learning

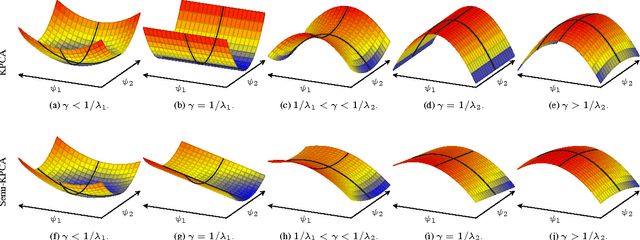
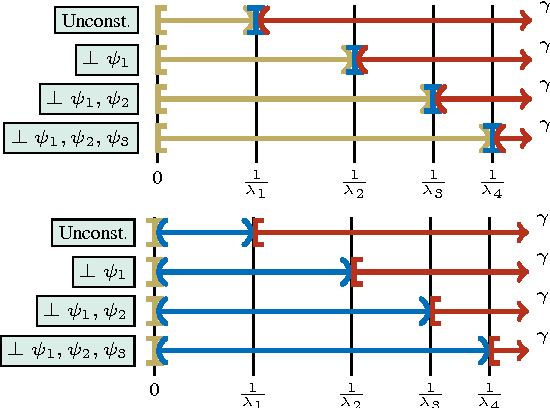
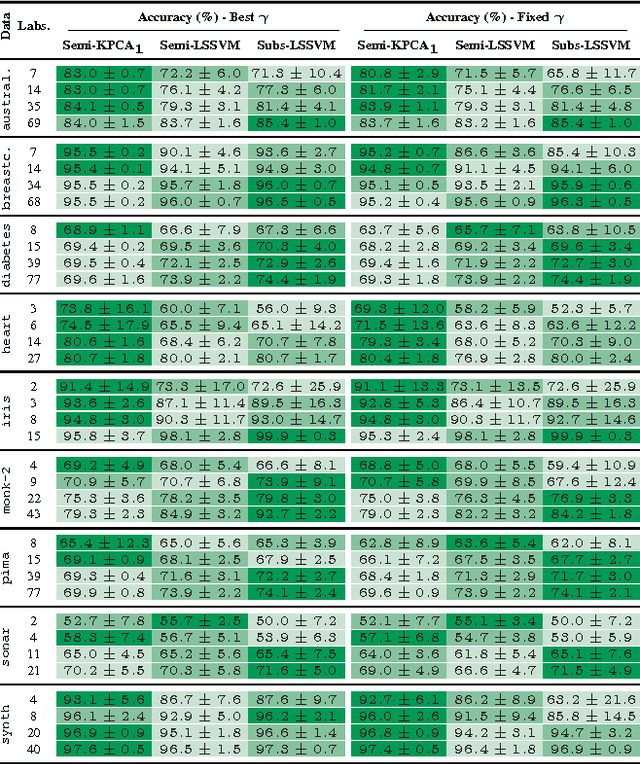
In this paper, Kernel PCA is reinterpreted as the solution to a convex optimization problem. Actually, there is a constrained convex problem for each principal component, so that the constraints guarantee that the principal component is indeed a solution, and not a mere saddle point. Although these insights do not imply any algorithmic improvement, they can be used to further understand the method, formulate possible extensions and properly address them. As an example, a new convex optimization problem for semi-supervised classification is proposed, which seems particularly well-suited whenever the number of known labels is small. Our formulation resembles a Least Squares SVM problem with a regularization parameter multiplied by a negative sign, combined with a variational principle for Kernel PCA. Our primal optimization principle for semi-supervised learning is solved in terms of the Lagrange multipliers. Numerical experiments in several classification tasks illustrate the performance of the proposed model in problems with only a few labeled data.