Robust Classification of Graph-Based Data
Paper and Code
Apr 27, 2018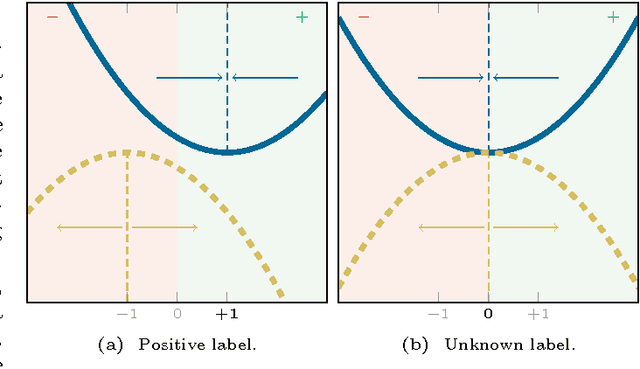
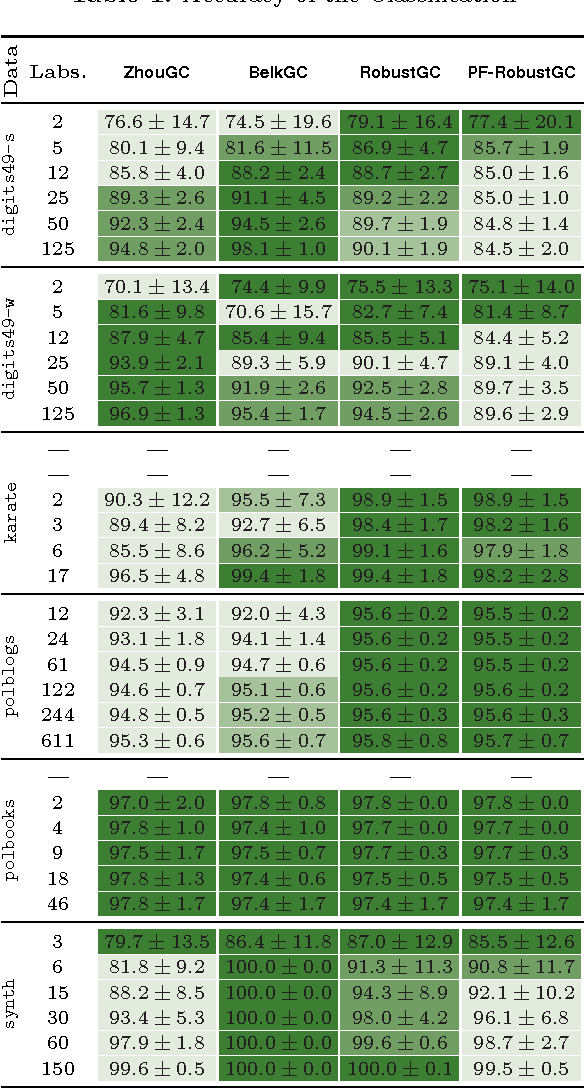
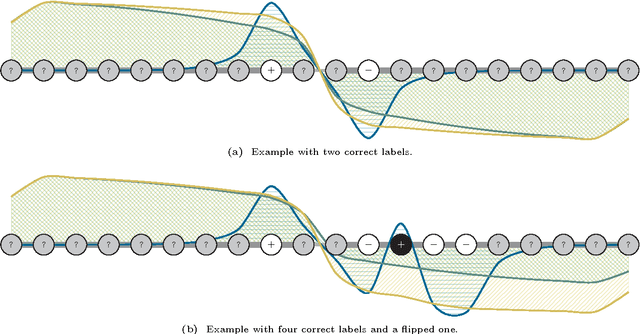
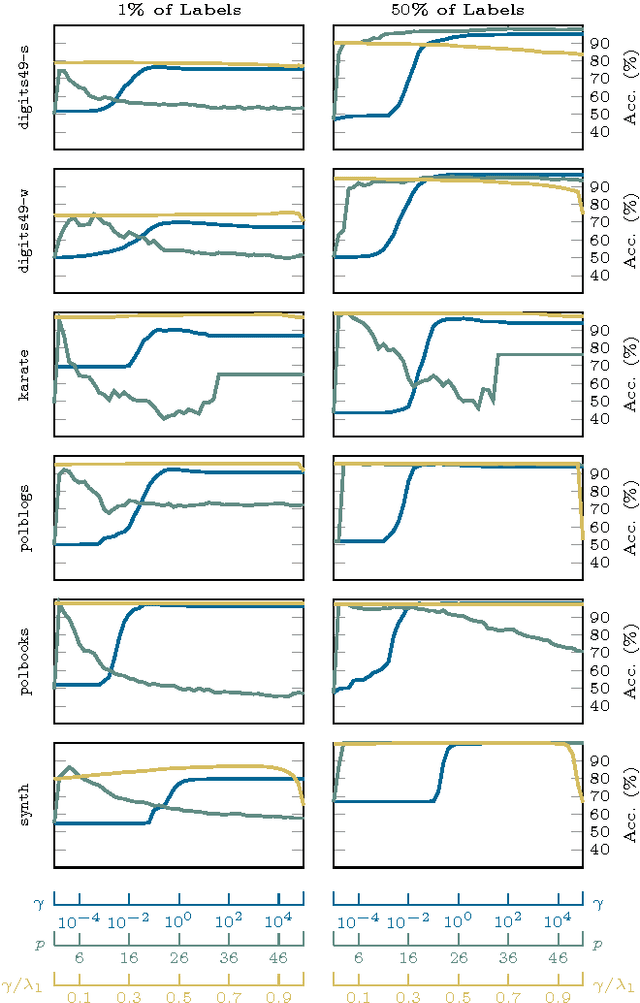
A graph-based classification method is proposed for semi-supervised learning in the case of Euclidean data and for classification in the case of graph data. Our manifold learning technique is based on a convex optimization problem involving a convex quadratic regularization term and a concave quadratic loss function with a trade-off parameter carefully chosen so that the objective function remains convex. As shown empirically, the advantage of considering a concave loss function is that the learning problem becomes more robust in the presence of noisy labels. Furthermore, the loss function considered here is then more similar to a classification loss while several other methods treat graph-based classification problems as regression problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge