Fault Detection in Induction Motors using Functional Dimensionality Reduction Methods

The implementation of strategies for fault detection and diagnosis on rotating electrical machines is crucial for the reliability and safety of modern industrial systems. The contribution of this work is a methodology that combines conventional strategy of Motor Current Signature Analysis with functional dimensionality reduction methods, namely Functional Principal Components Analysis and Functional Diffusion Maps, for detecting and classifying fault conditions in induction motors. The results obtained from the proposed scheme are very encouraging, revealing a potential use in the future not only for real-time detection of the presence of a fault in an induction motor, but also in the identification of a greater number of types of faults present through an offline analysis.

Functional Diffusion Maps

Nowadays many real-world datasets can be considered as functional, in the sense that the processes which generate them are continuous. A fundamental property of this type of data is that in theory they belong to an infinite-dimensional space. Although in practice we usually receive finite observations, they are still high-dimensional and hence dimensionality reduction methods are crucial. In this vein, the main state-of-the-art method for functional data analysis is Functional PCA. Nevertheless, this classic technique assumes that the data lie in a linear manifold, and hence it could have problems when this hypothesis is not fulfilled. In this research, attention has been placed on a non-linear manifold learning method: Diffusion Maps. The article explains how to extend this multivariate method to functional data and compares its behavior against Functional PCA over different simulated and real examples.

Auto-adaptative Laplacian Pyramids for High-dimensional Data Analysis

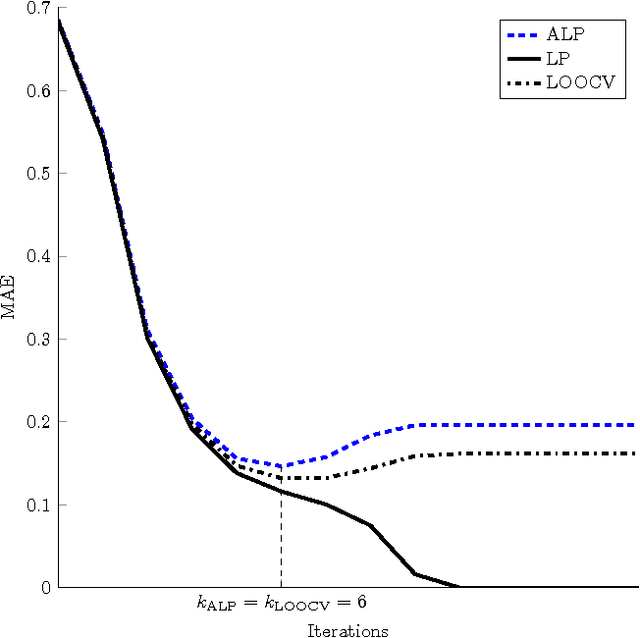
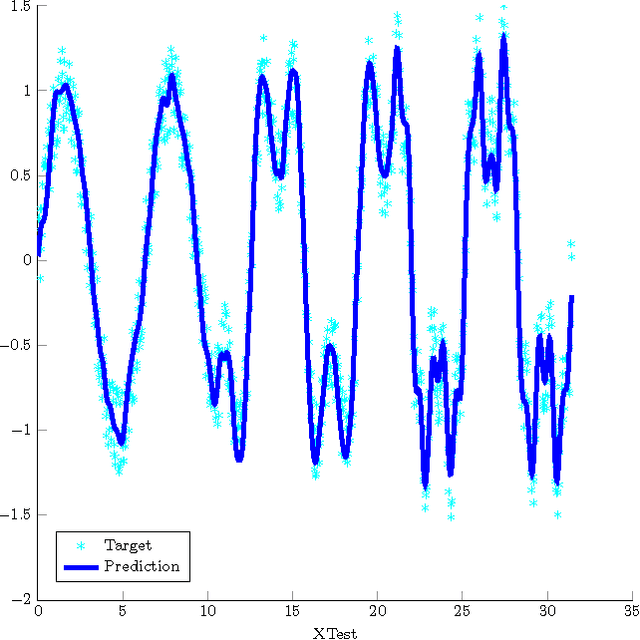
Non-linear dimensionality reduction techniques such as manifold learning algorithms have become a common way for processing and analyzing high-dimensional patterns that often have attached a target that corresponds to the value of an unknown function. Their application to new points consists in two steps: first, embedding the new data point into the low dimensional space and then, estimating the function value on the test point from its neighbors in the embedded space. However, finding the low dimension representation of a test point, while easy for simple but often not powerful enough procedures such as PCA, can be much more complicated for methods that rely on some kind of eigenanalysis, such as Spectral Clustering (SC) or Diffusion Maps (DM). Similarly, when a target function is to be evaluated, averaging methods like nearest neighbors may give unstable results if the function is noisy. Thus, the smoothing of the target function with respect to the intrinsic, low-dimensional representation that describes the geometric structure of the examined data is a challenging task. In this paper we propose Auto-adaptive Laplacian Pyramids (ALP), an extension of the standard Laplacian Pyramids model that incorporates a modified LOOCV procedure that avoids the large cost of the standard one and offers the following advantages: (i) it selects automatically the optimal function resolution (stopping time) adapted to the data and its noise, (ii) it is easy to apply as it does not require parameterization, (iii) it does not overfit the training set and (iv) it adds no extra cost compared to other classical interpolation methods. We illustrate numerically ALP's behavior on a synthetic problem and apply it to the computation of the DM projection of new patterns and to the extension to them of target function values on a radiation forecasting problem over very high dimensional patterns.