Graph-based Extreme Feature Selection for Multi-class Classification Tasks

When processing high-dimensional datasets, a common pre-processing step is feature selection. Filter-based feature selection algorithms are not tailored to a specific classification method, but rather rank the relevance of each feature with respect to the target and the task. This work focuses on a graph-based, filter feature selection method that is suited for multi-class classifications tasks. We aim to drastically reduce the number of selected features, in order to create a sketch of the original data that codes valuable information for the classification task. The proposed graph-based algorithm is constructed by combing the Jeffries-Matusita distance with a non-linear dimension reduction method, diffusion maps. Feature elimination is performed based on the distribution of the features in the low-dimensional space. Then, a very small number of feature that have complementary separation strengths, are selected. Moreover, the low-dimensional embedding allows to visualize the feature space. Experimental results are provided for public datasets and compared with known filter-based feature selection techniques.

Multi-View Kernels for Low-Dimensional Modeling of Seismic Events

The problem of learning from seismic recordings has been studied for years. There is a growing interest in developing automatic mechanisms for identifying the properties of a seismic event. One main motivation is the ability have a reliable identification of man-made explosions. The availability of multiple high-dimensional observations has increased the use of machine learning techniques in a variety of fields. In this work, we propose to use a kernel-fusion based dimensionality reduction framework for generating meaningful seismic representations from raw data. The proposed method is tested on 2023 events that were recorded in Israel and in Jordan. The method achieves promising results in classification of event type as well as in estimating the location of the event. The proposed fusion and dimensionality reduction tools may be applied to other types of geophysical data.

Auto-adaptative Laplacian Pyramids for High-dimensional Data Analysis

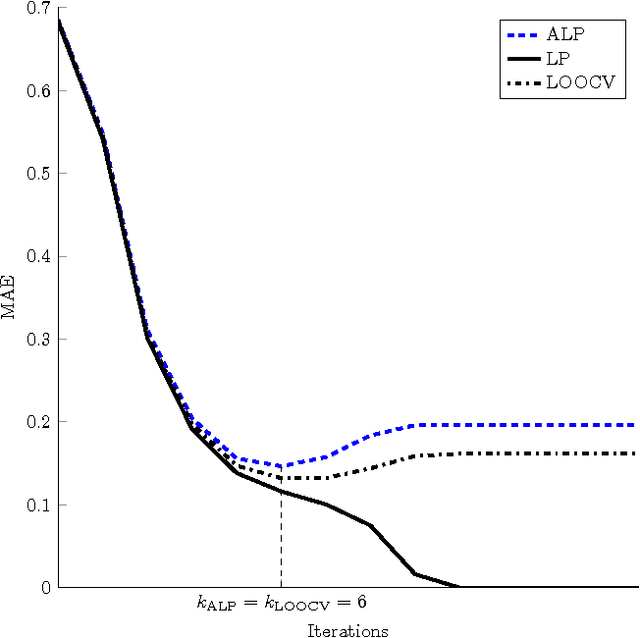
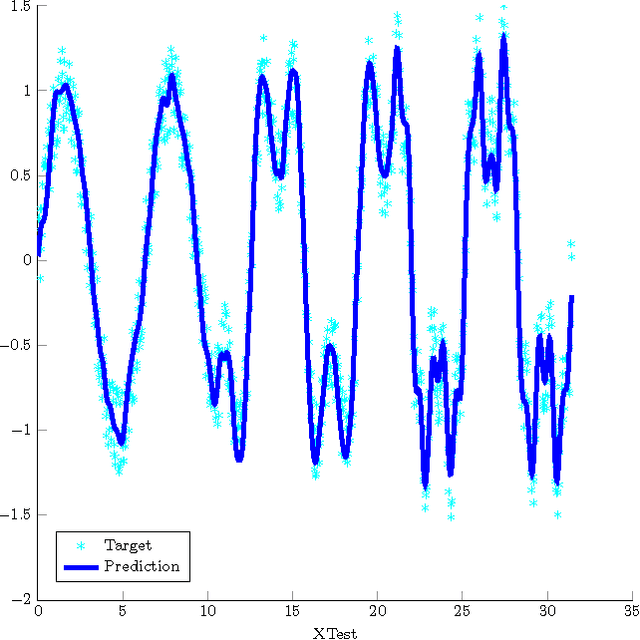
Non-linear dimensionality reduction techniques such as manifold learning algorithms have become a common way for processing and analyzing high-dimensional patterns that often have attached a target that corresponds to the value of an unknown function. Their application to new points consists in two steps: first, embedding the new data point into the low dimensional space and then, estimating the function value on the test point from its neighbors in the embedded space. However, finding the low dimension representation of a test point, while easy for simple but often not powerful enough procedures such as PCA, can be much more complicated for methods that rely on some kind of eigenanalysis, such as Spectral Clustering (SC) or Diffusion Maps (DM). Similarly, when a target function is to be evaluated, averaging methods like nearest neighbors may give unstable results if the function is noisy. Thus, the smoothing of the target function with respect to the intrinsic, low-dimensional representation that describes the geometric structure of the examined data is a challenging task. In this paper we propose Auto-adaptive Laplacian Pyramids (ALP), an extension of the standard Laplacian Pyramids model that incorporates a modified LOOCV procedure that avoids the large cost of the standard one and offers the following advantages: (i) it selects automatically the optimal function resolution (stopping time) adapted to the data and its noise, (ii) it is easy to apply as it does not require parameterization, (iii) it does not overfit the training set and (iv) it adds no extra cost compared to other classical interpolation methods. We illustrate numerically ALP's behavior on a synthetic problem and apply it to the computation of the DM projection of new patterns and to the extension to them of target function values on a radiation forecasting problem over very high dimensional patterns.