Convex Formulation for Kernel PCA and its Use in Semi-Supervised Learning
Paper and Code
Oct 21, 2016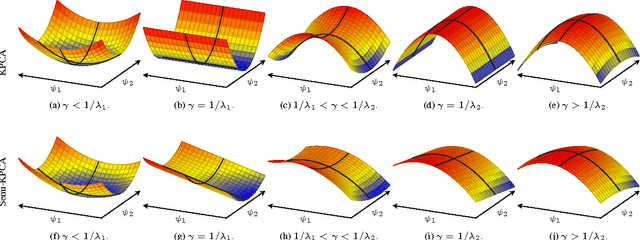
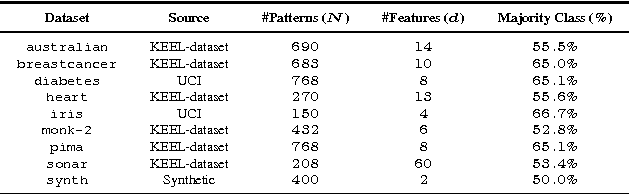
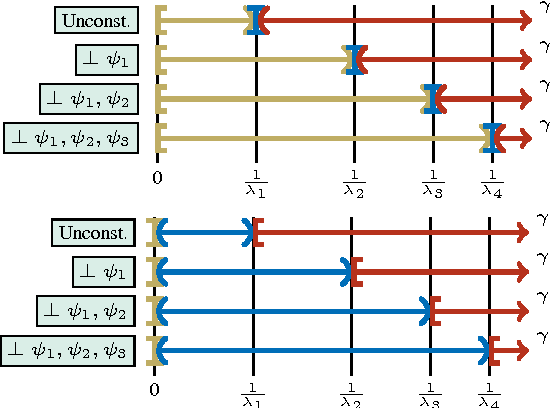
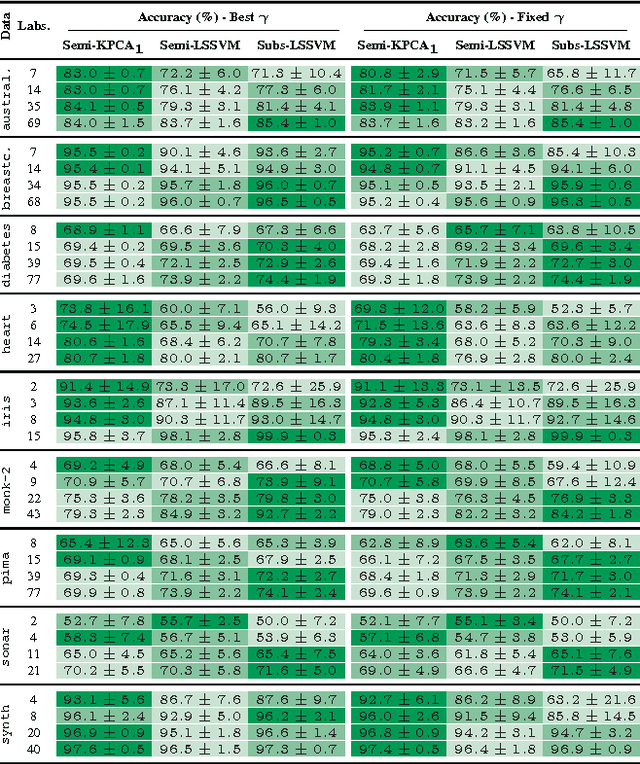
In this paper, Kernel PCA is reinterpreted as the solution to a convex optimization problem. Actually, there is a constrained convex problem for each principal component, so that the constraints guarantee that the principal component is indeed a solution, and not a mere saddle point. Although these insights do not imply any algorithmic improvement, they can be used to further understand the method, formulate possible extensions and properly address them. As an example, a new convex optimization problem for semi-supervised classification is proposed, which seems particularly well-suited whenever the number of known labels is small. Our formulation resembles a Least Squares SVM problem with a regularization parameter multiplied by a negative sign, combined with a variational principle for Kernel PCA. Our primal optimization principle for semi-supervised learning is solved in terms of the Lagrange multipliers. Numerical experiments in several classification tasks illustrate the performance of the proposed model in problems with only a few labeled data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge