A Survey on Solving and Discovering Differential Equations Using Deep Neural Networks

Ordinary and partial differential equations (DE) are used extensively in scientific and mathematical domains to model physical systems. Current literature has focused primarily on deep neural network (DNN) based methods for solving a specific DE or a family of DEs. Research communities with a history of using DE models may view DNN-based differential equation solvers (DNN-DEs) as a faster and transferable alternative to current numerical methods. However, there is a lack of systematic surveys detailing the use of DNN-DE methods across physical application domains and a generalized taxonomy to guide future research. This paper surveys and classifies previous works and provides an educational tutorial for senior practitioners, professionals, and graduate students in engineering and computer science. First, we propose a taxonomy to navigate domains of DE systems studied under the umbrella of DNN-DE. Second, we examine the theory and performance of the Physics Informed Neural Network (PINN) to demonstrate how the influential DNN-DE architecture mathematically solves a system of equations. Third, to reinforce the key ideas of solving and discovery of DEs using DNN, we provide a tutorial using DeepXDE, a Python package for developing PINNs, to develop DNN-DEs for solving and discovering a classic DE, the linear transport equation.

MC-DGCNN: A Novel DNN Architecture for Multi-Category Point Set Classification

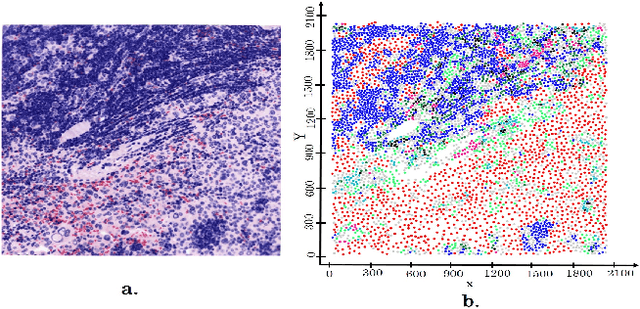
Point set classification aims to build a representation learning model that distinguishes between spatial and categorical configurations of point set data. This problem is societally important since in many applications domains such as immunology, and microbial ecology. This problem is challenging since the interactions between different categories of points are not always equal; as a result, the representation learning model must selectively learn the most relevant multi-categorical relationships. The related works are limited (1) in learning the importance of different multi-categorical relationships, especially for high-order interactions, and (2) do not fully exploit the spatial distribution of points beyond simply measuring relative distance or applying a feed-forward neural network to coordinates. To overcome these limitations, we leverage the dynamic graph convolutional neural network (DGCNN) architecture to design a novel multi-category DGCNN (MC-DGCNN), contributing location representation and point pair attention layers for multi-categorical point set classification. MC-DGCNN has the ability to identify the categorical importance of each point pair and extends this to N-way spatial relationships, while still preserving all the properties and benefits of DGCNN (e.g., differentiability). Experimental results show that the proposed architecture is computationally efficient and significantly outperforms current deep learning architectures on real-world datasets.

Towards Comparative Physical Interpretation of Spatial Variability Aware Neural Networks: A Summary of Results

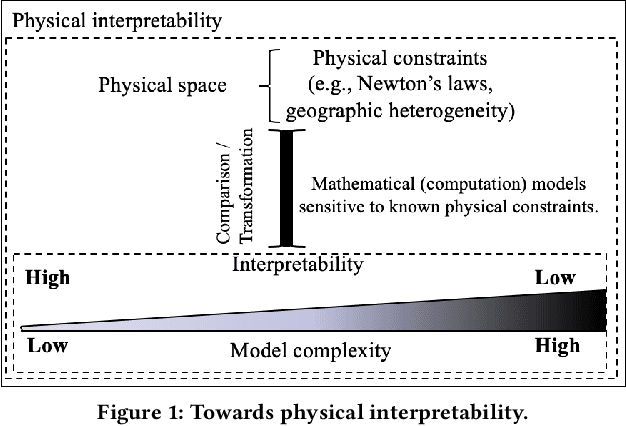
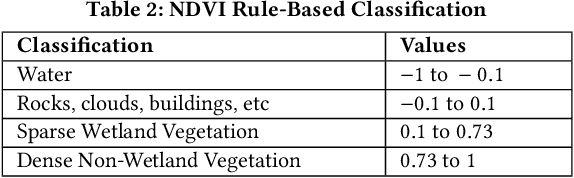
Given Spatial Variability Aware Neural Networks (SVANNs), the goal is to investigate mathematical (or computational) models for comparative physical interpretation towards their transparency (e.g., simulatibility, decomposability and algorithmic transparency). This problem is important due to important use-cases such as reusability, debugging, and explainability to a jury in a court of law. Challenges include a large number of model parameters, vacuous bounds on generalization performance of neural networks, risk of overfitting, sensitivity to noise, etc., which all detract from the ability to interpret the models. Related work on either model-specific or model-agnostic post-hoc interpretation is limited due to a lack of consideration of physical constraints (e.g., mass balance) and properties (e.g., second law of geography). This work investigates physical interpretation of SVANNs using novel comparative approaches based on geographically heterogeneous features. The proposed approach on feature-based physical interpretation is evaluated using a case-study on wetland mapping. The proposed physical interpretation improves the transparency of SVANN models and the analytical results highlight the trade-off between model transparency and model performance (e.g., F1-score). We also describe an interpretation based on geographically heterogeneous processes modeled as partial differential equations (PDEs).