Physics-based machine learning framework for predicting NOx emissions from compression ignition engines using on-board diagnostics data

This work presents a physics-based machine learning framework to predict and analyze oxides of nitrogen (NOx) emissions from compression-ignition engine-powered vehicles using on-board diagnostics (OBD) data as input. Accurate NOx prediction from OBD datasets is difficult because NOx formation inside an engine combustion chamber is governed by complex processes occurring on timescales much shorter than the data collection rate. Thus, emissions generally cannot be predicted accurately using simple empirically derived physics models. Black box models like genetic algorithms or neural networks can be more accurate, but have poor interpretability. The transparent model presented in this paper has both high accuracy and can explain potential sources of high emissions. The proposed framework consists of two major steps: a physics-based NOx prediction model combined with a novel Divergent Window Co-occurrence (DWC) Pattern detection algorithm to analyze operating conditions that are not adequately addressed by the physics-based model. The proposed framework is validated for generalizability with a second vehicle OBD dataset, a sensitivity analysis is performed, and model predictions are compared with that from a deep neural network. The results show that NOx emissions predictions using the proposed model has around 55% better root mean square error, and around 60% higher mean absolute error compared to the baseline NOx prediction model from previously published work. The DWC Pattern Detection Algorithm identified low engine power conditions to have high statistical significance, indicating an operating regime where the model can be improved. This work shows that the physics-based machine learning framework is a viable method for predicting NOx emissions from engines that do not incorporate NOx sensing.

A Survey on Solving and Discovering Differential Equations Using Deep Neural Networks

Ordinary and partial differential equations (DE) are used extensively in scientific and mathematical domains to model physical systems. Current literature has focused primarily on deep neural network (DNN) based methods for solving a specific DE or a family of DEs. Research communities with a history of using DE models may view DNN-based differential equation solvers (DNN-DEs) as a faster and transferable alternative to current numerical methods. However, there is a lack of systematic surveys detailing the use of DNN-DE methods across physical application domains and a generalized taxonomy to guide future research. This paper surveys and classifies previous works and provides an educational tutorial for senior practitioners, professionals, and graduate students in engineering and computer science. First, we propose a taxonomy to navigate domains of DE systems studied under the umbrella of DNN-DE. Second, we examine the theory and performance of the Physics Informed Neural Network (PINN) to demonstrate how the influential DNN-DE architecture mathematically solves a system of equations. Third, to reinforce the key ideas of solving and discovery of DEs using DNN, we provide a tutorial using DeepXDE, a Python package for developing PINNs, to develop DNN-DEs for solving and discovering a classic DE, the linear transport equation.

Vehicle Emissions Prediction with Physics-Aware AI Models: Preliminary Results

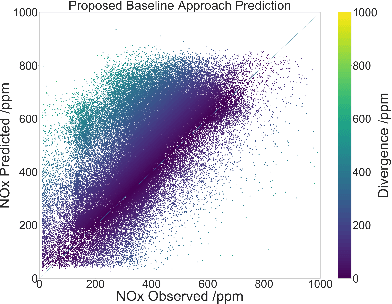
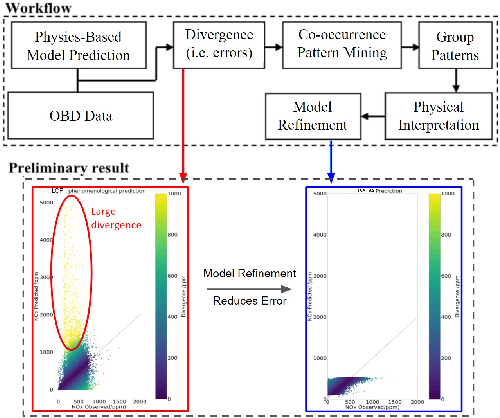
Given an on-board diagnostics (OBD) dataset and a physics-based emissions prediction model, this paper aims to develop an accurate and computational-efficient AI (Artificial Intelligence) method that predicts vehicle emissions. The problem is of societal importance because vehicular emissions lead to climate change and impact human health. This problem is challenging because the OBD data does not contain enough parameters needed by high-order physics models. Conversely, related work has shown that low-order physics models have poor predictive accuracy when using available OBD data. This paper uses a divergent window co-occurrence pattern detection method to develop a spatiotemporal variability-aware AI model for predicting emission values from the OBD datasets. We conducted a case study using real-world OBD data from a local public transportation agency. Results show that the proposed AI method has approximately 65% improved predictive accuracy than a non-AI low-order physics model and is approximately 35% more accurate than a baseline model.