Combining Machine Learning and Agent-Based Modeling to Study Biomedical Systems

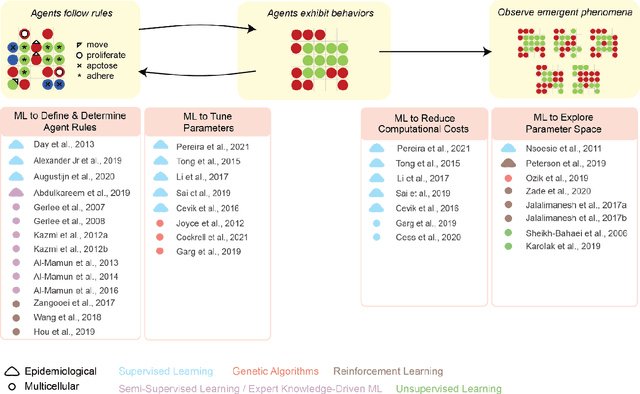
Agent-based modeling (ABM) is a well-established paradigm for simulating complex systems via interactions between constituent entities. Machine learning (ML) refers to approaches whereby statistical algorithms 'learn' from data on their own, without imposing a priori theories of system behavior. Biological systems -- from molecules, to cells, to entire organisms -- consist of vast numbers of entities, governed by complex webs of interactions that span many spatiotemporal scales and exhibit nonlinearity, stochasticity and intricate coupling between entities. The macroscopic properties and collective dynamics of such systems are difficult to capture via continuum modelling and mean-field formalisms. ABM takes a 'bottom-up' approach that obviates these difficulties by enabling one to easily propose and test a set of well-defined 'rules' to be applied to the individual entities (agents) in a system. Evaluating a system and propagating its state over discrete time-steps effectively simulates the system, allowing observables to be computed and system properties to be analyzed. Because the rules that govern an ABM can be difficult to abstract and formulate from experimental data, there is an opportunity to use ML to help infer optimal, system-specific ABM rules. Once such rule-sets are devised, ABM calculations can generate a wealth of data, and ML can be applied there too -- e.g., to probe statistical measures that meaningfully describe a system's stochastic properties. As an example of synergy in the other direction (from ABM to ML), ABM simulations can generate realistic datasets for training ML algorithms (e.g., for regularization, to mitigate overfitting). In these ways, one can envision various synergistic ABM$\rightleftharpoons$ML loops. This review summarizes how ABM and ML have been integrated in contexts that span spatial scales from the cellular to population-level scale epidemiology.

Exploration of Dark Chemical Genomics Space via Portal Learning: Applied to Targeting the Undruggable Genome and COVID-19 Anti-Infective Polypharmacology

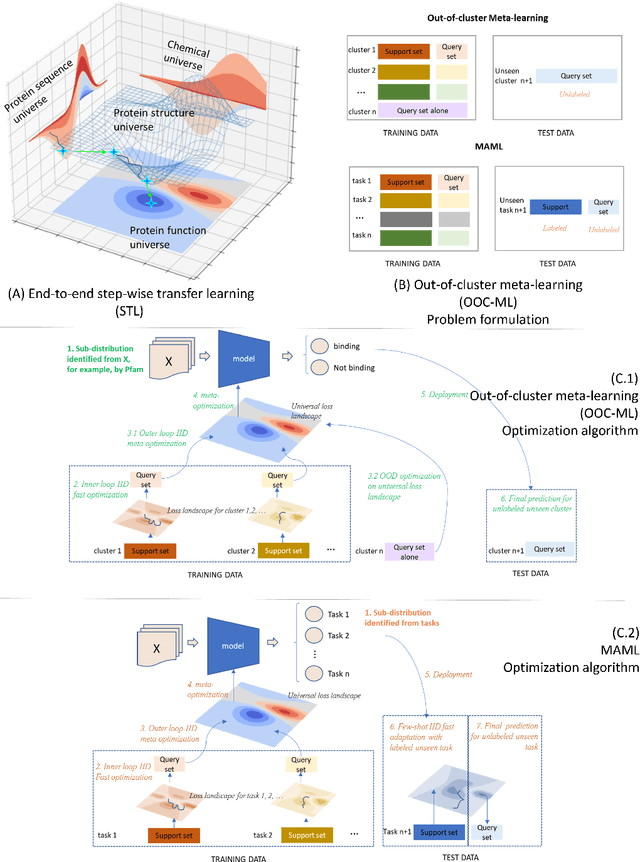
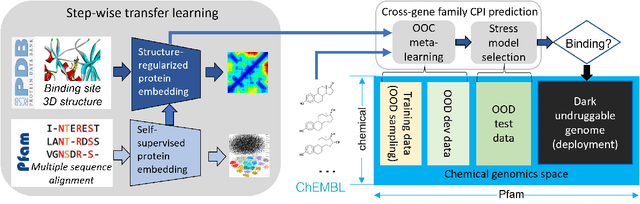
Advances in biomedicine are largely fueled by exploring uncharted territories of human biology. Machine learning can both enable and accelerate discovery, but faces a fundamental hurdle when applied to unseen data with distributions that differ from previously observed ones -- a common dilemma in scientific inquiry. We have developed a new deep learning framework, called {\textit{Portal Learning}}, to explore dark chemical and biological space. Three key, novel components of our approach include: (i) end-to-end, step-wise transfer learning, in recognition of biology's sequence-structure-function paradigm, (ii) out-of-cluster meta-learning, and (iii) stress model selection. Portal Learning provides a practical solution to the out-of-distribution (OOD) problem in statistical machine learning. Here, we have implemented Portal Learning to predict chemical-protein interactions on a genome-wide scale. Systematic studies demonstrate that Portal Learning can effectively assign ligands to unexplored gene families (unknown functions), versus existing state-of-the-art methods, thereby allowing us to target previously "undruggable" proteins and design novel polypharmacological agents for disrupting interactions between SARS-CoV-2 and human proteins. Portal Learning is general-purpose and can be further applied to other areas of scientific inquiry.

Machine Learning for Classification of Protein Helix Capping Motifs

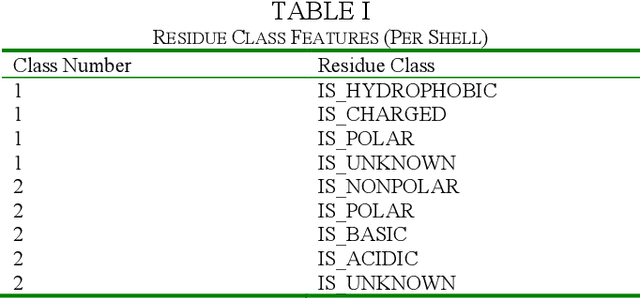
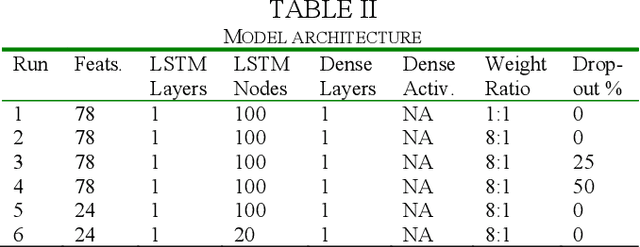
The biological function of a protein stems from its 3-dimensional structure, which is thermodynamically determined by the energetics of interatomic forces between its amino acid building blocks (the order of amino acids, known as the sequence, defines a protein). Given the costs (time, money, human resources) of determining protein structures via experimental means such as X-ray crystallography, can we better describe and compare protein 3D structures in a robust and efficient manner, so as to gain meaningful biological insights? We begin by considering a relatively simple problem, limiting ourselves to just protein secondary structural elements. Historically, many computational methods have been devised to classify amino acid residues in a protein chain into one of several discrete secondary structures, of which the most well-characterized are the geometrically regular $\alpha$-helix and $\beta$-sheet; irregular structural patterns, such as 'turns' and 'loops', are less understood. Here, we present a study of Deep Learning techniques to classify the loop-like end cap structures which delimit $\alpha$-helices. Previous work used highly empirical and heuristic methods to manually classify helix capping motifs. Instead, we use structural data directly--including (i) backbone torsion angles computed from 3D structures, (ii) macromolecular feature sets (e.g., physicochemical properties), and (iii) helix cap classification data (from CAPS-DB)--as the ground truth to train a bidirectional long short-term memory (BiLSTM) model to classify helix cap residues. We tried different network architectures and scanned hyperparameters in order to train and assess several models; we also trained a Support Vector Classifier (SVC) to use as a baseline. Ultimately, we achieved 85% class-balanced accuracy with a deep BiLSTM model.