SparCML: High-Performance Sparse Communication for Machine Learning

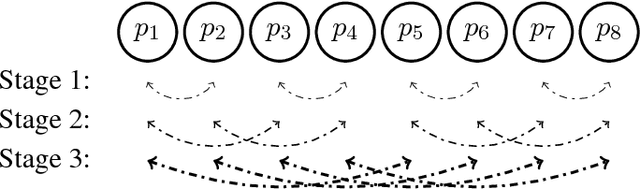
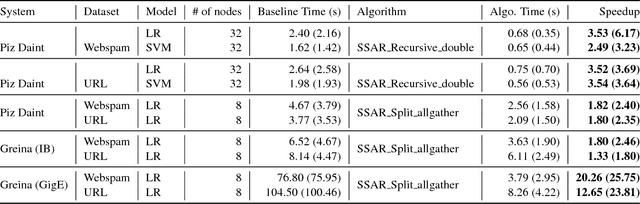
One of the main drivers behind the rapid recent advances in machine learning has been the availability of efficient system support. Despite existing progress, scaling compute-intensive machine learning workloads to a large number of compute nodes is still a challenging task. In this paper, we address this challenge, by proposing SparCML, a general, scalable communication layer for machine learning applications. SparCML is built on the observation that many distributed machine learning algorithms either have naturally sparse communication patterns, or have updates which can be sparsified in a structured way for improved performance, without loss of convergence or accuracy. To exploit this insight, we analyze, design, and implement a set of communication-efficient protocols for sparse input data, in conjunction with efficient machine learning algorithms which can leverage these primitives. Our communication protocols generalize standard collective operations, by allowing processes to contribute sparse input data vectors, of heterogeneous sizes. Our generic communication layer is enriched with additional features, such as support for non-blocking (asynchronous) operations and support for low-precision data representations. We validate our algorithmic results experimentally on a range of large-scale machine learning applications and target architectures, showing that we can leverage sparsity for order-of-magnitude runtime savings, compared to existing methods and frameworks.

The Convergence of Sparsified Gradient Methods

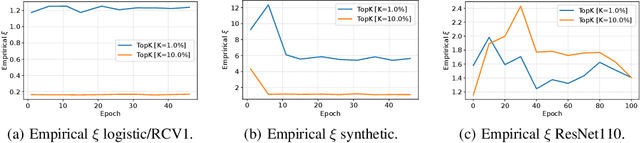
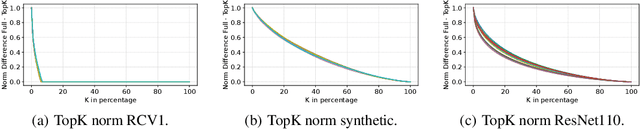
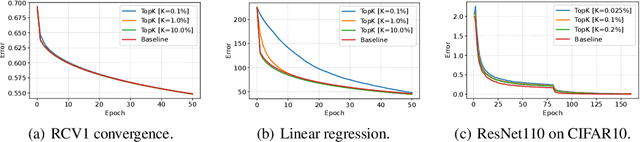
Distributed training of massive machine learning models, in particular deep neural networks, via Stochastic Gradient Descent (SGD) is becoming commonplace. Several families of communication-reduction methods, such as quantization, large-batch methods, and gradient sparsification, have been proposed. To date, gradient sparsification methods - where each node sorts gradients by magnitude, and only communicates a subset of the components, accumulating the rest locally - are known to yield some of the largest practical gains. Such methods can reduce the amount of communication per step by up to three orders of magnitude, while preserving model accuracy. Yet, this family of methods currently has no theoretical justification. This is the question we address in this paper. We prove that, under analytic assumptions, sparsifying gradients by magnitude with local error correction provides convergence guarantees, for both convex and non-convex smooth objectives, for data-parallel SGD. The main insight is that sparsification methods implicitly maintain bounds on the maximum impact of stale updates, thanks to selection by magnitude. Our analysis and empirical validation also reveal that these methods do require analytical conditions to converge well, justifying existing heuristics.