SMC Is All You Need: Parallel Strong Scaling

In the general framework of Bayesian inference, the target distribution can only be evaluated up-to a constant of proportionality. Classical consistent Bayesian methods such as sequential Monte Carlo (SMC) and Markov chain Monte Carlo (MCMC) have unbounded time complexity requirements. We develop a fully parallel sequential Monte Carlo (pSMC) method which provably delivers parallel strong scaling, i.e. the time complexity (and per-node memory) remains bounded if the number of asynchronous processes is allowed to grow. More precisely, the pSMC has a theoretical convergence rate of MSE$ = O(1/NR)$, where $N$ denotes the number of communicating samples in each processor and $R$ denotes the number of processors. In particular, for suitably-large problem-dependent $N$, as $R \rightarrow \infty$ the method converges to infinitesimal accuracy MSE$=O(\varepsilon^2)$ with a fixed finite time-complexity Cost$=O(1)$ and with no efficiency leakage, i.e. computational complexity Cost$=O(\varepsilon^{-2})$. A number of Bayesian inference problems are taken into consideration to compare the pSMC and MCMC methods.

Demonstration of machine-learning-enhanced Bayesian quantum state estimation

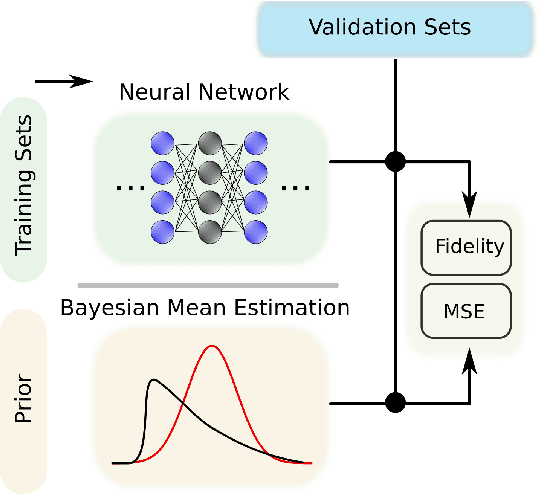
Machine learning (ML) has found broad applicability in quantum information science in topics as diverse as experimental design, state classification, and even studies on quantum foundations. Here, we experimentally realize an approach for defining custom prior distributions that are automatically tuned using ML for use with Bayesian quantum state estimation methods. Previously, researchers have looked to Bayesian quantum state tomography due to its unique advantages like natural uncertainty quantification, the return of reliable estimates under any measurement condition, and minimal mean-squared error. However, practical challenges related to long computation times and conceptual issues concerning how to incorporate prior knowledge most suitably can overshadow these benefits. Using both simulated and experimental measurement results, we demonstrate that ML-defined prior distributions reduce net convergence times and provide a natural way to incorporate both implicit and explicit information directly into the prior distribution. These results constitute a promising path toward practical implementations of Bayesian quantum state tomography.

Deep learning for enhanced free-space optical communications

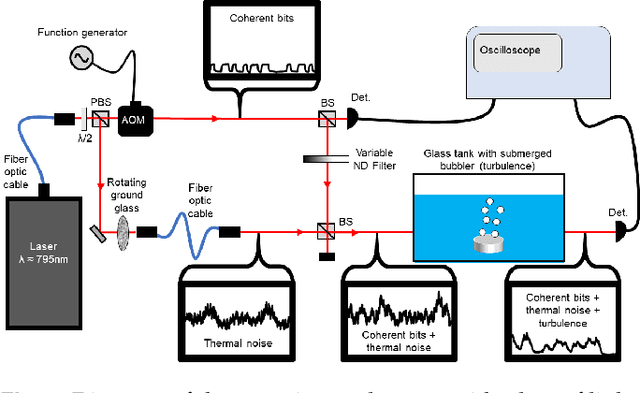
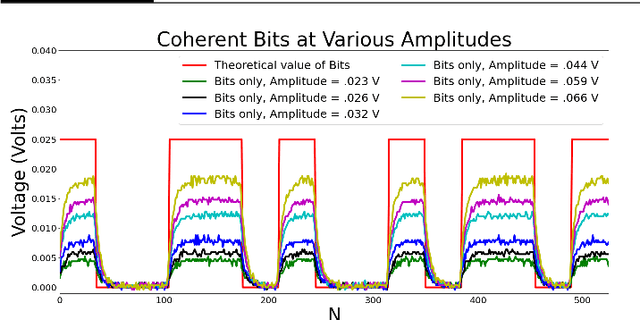
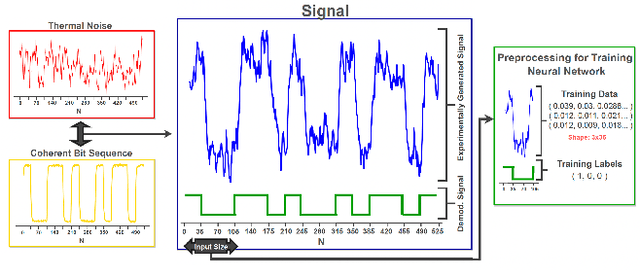
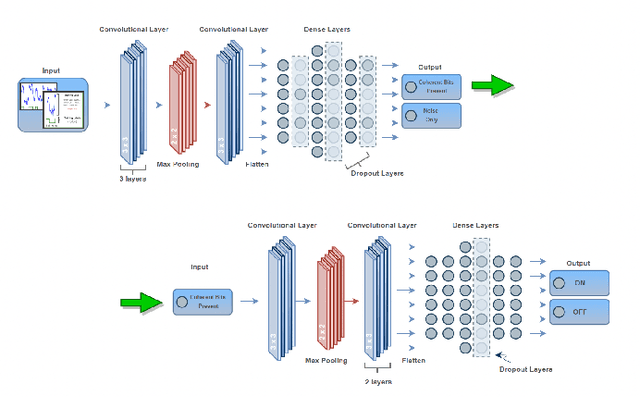
Atmospheric effects, such as turbulence and background thermal noise, inhibit the propagation of coherent light used in ON-OFF keying free-space optical communication. Here we present and experimentally validate a convolutional neural network to reduce the bit error rate of free-space optical communication in post-processing that is significantly simpler and cheaper than existing solutions based on advanced optics. Our approach consists of two neural networks, the first determining the presence of coherent bit sequences in thermal noise and turbulence and the second demodulating the coherent bit sequences. All data used for training and testing our network is obtained experimentally by generating ON-OFF keying bit streams of coherent light, combining these with thermal light, and passing the resultant light through a turbulent water tank which we have verified mimics turbulence in the air to a high degree of accuracy. Our convolutional neural network improves detection accuracy over threshold classification schemes and has the capability to be integrated with current demodulation and error correction schemes.

Dimension-adaptive machine-learning-based quantum state reconstruction

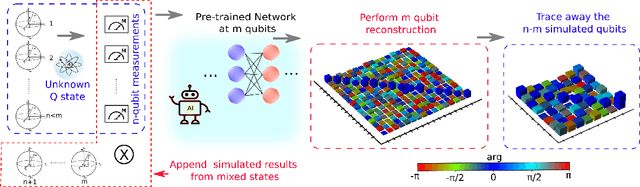
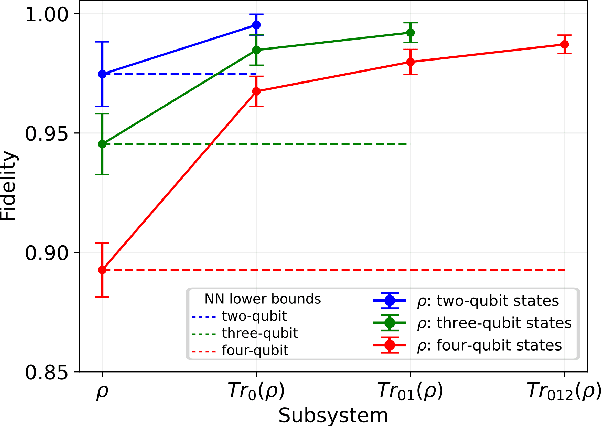
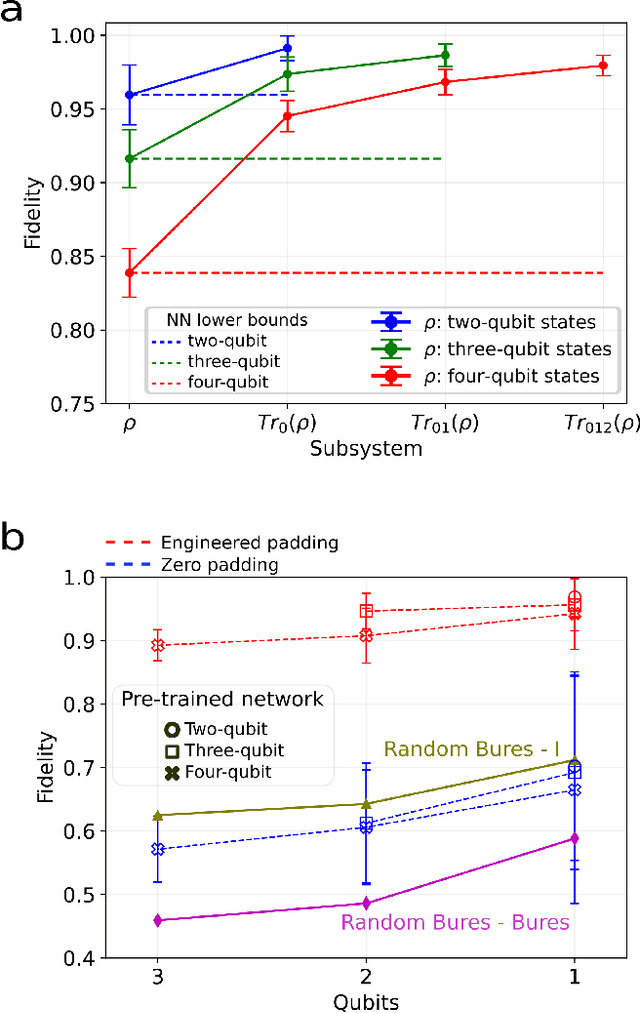
We introduce an approach for performing quantum state reconstruction on systems of $n$ qubits using a machine-learning-based reconstruction system trained exclusively on $m$ qubits, where $m\geq n$. This approach removes the necessity of exactly matching the dimensionality of a system under consideration with the dimension of a model used for training. We demonstrate our technique by performing quantum state reconstruction on randomly sampled systems of one, two, and three qubits using machine-learning-based methods trained exclusively on systems containing at least one additional qubit. The reconstruction time required for machine-learning-based methods scales significantly more favorably than the training time; hence this technique can offer an overall savings of resources by leveraging a single neural network for dimension-variable state reconstruction, obviating the need to train dedicated machine-learning systems for each Hilbert space.

Data-Centric Machine Learning in Quantum Information Science

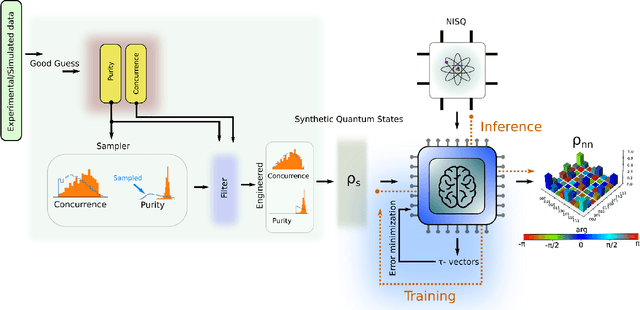
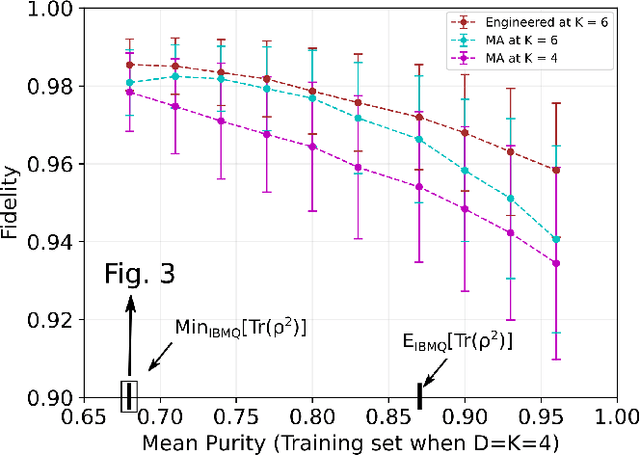
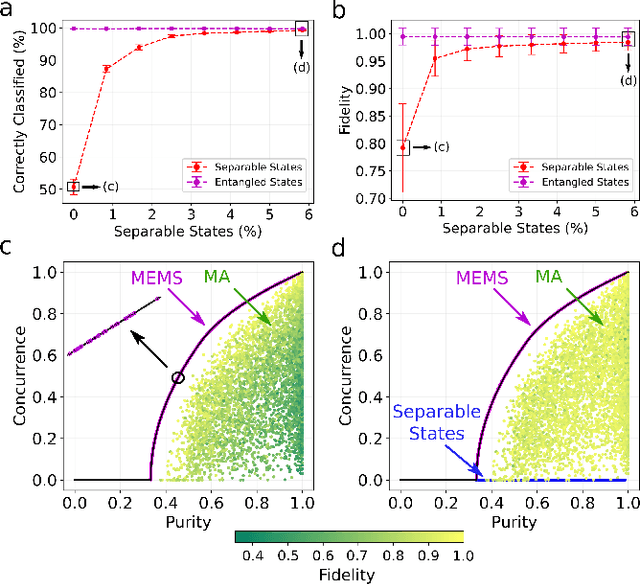
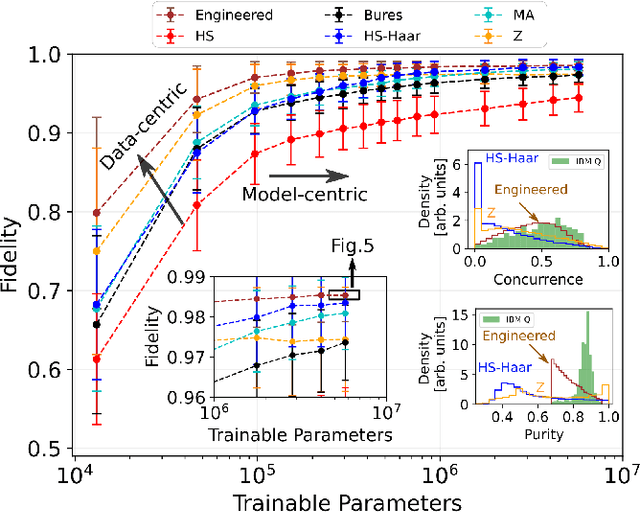
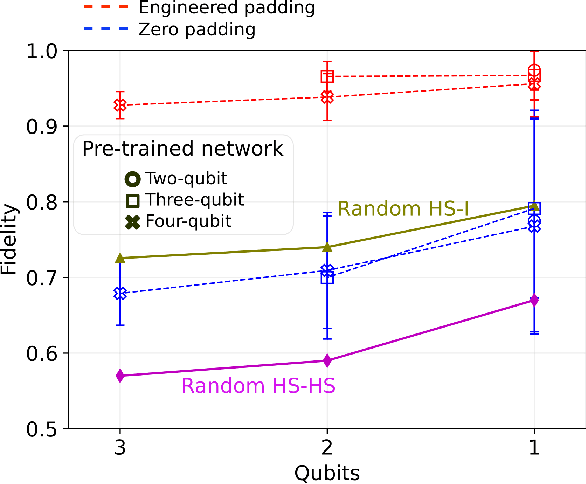
We propose a series of data-centric heuristics for improving the performance of machine learning systems when applied to problems in quantum information science. In particular, we consider how systematic engineering of training sets can significantly enhance the accuracy of pre-trained neural networks used for quantum state reconstruction without altering the underlying architecture. We find that it is not always optimal to engineer training sets to exactly match the expected distribution of a target scenario, and instead, performance can be further improved by biasing the training set to be slightly more mixed than the target. This is due to the heterogeneity in the number of free variables required to describe states of different purity, and as a result, overall accuracy of the network improves when training sets of a fixed size focus on states with the least constrained free variables. For further clarity, we also include a "toy model" demonstration of how spurious correlations can inadvertently enter synthetic data sets used for training, how the performance of systems trained with these correlations can degrade dramatically, and how the inclusion of even relatively few counterexamples can effectively remedy such problems.

Improving application performance with biased distributions of quantum states

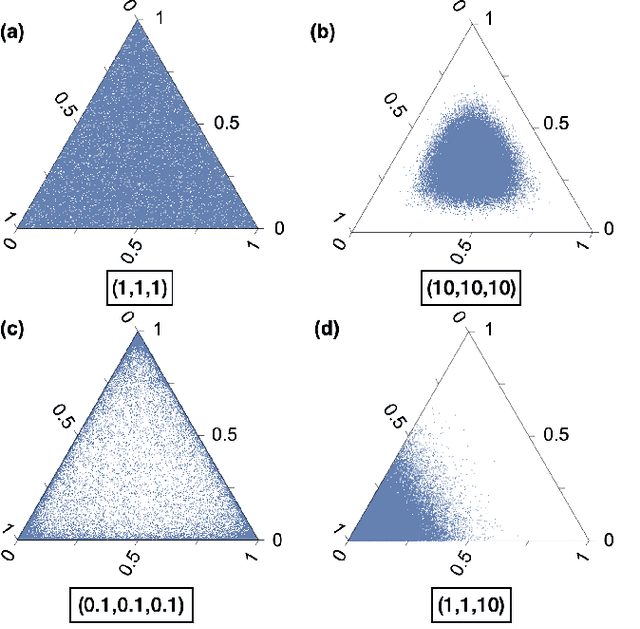
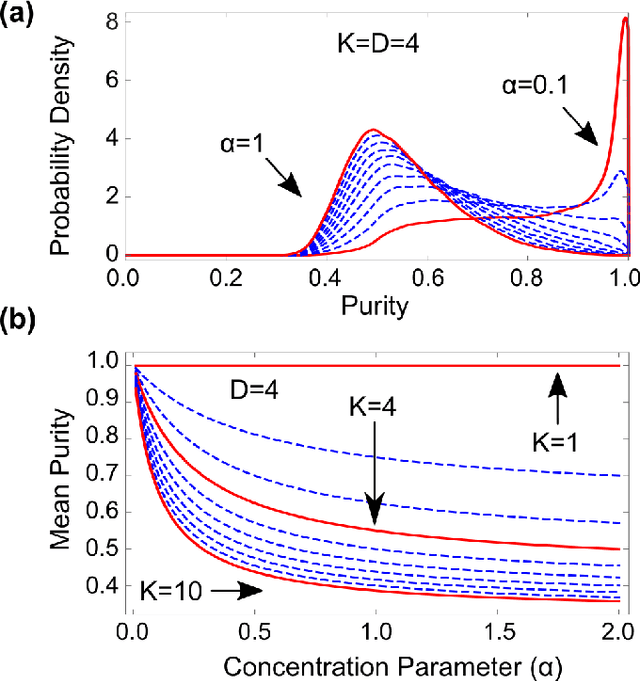
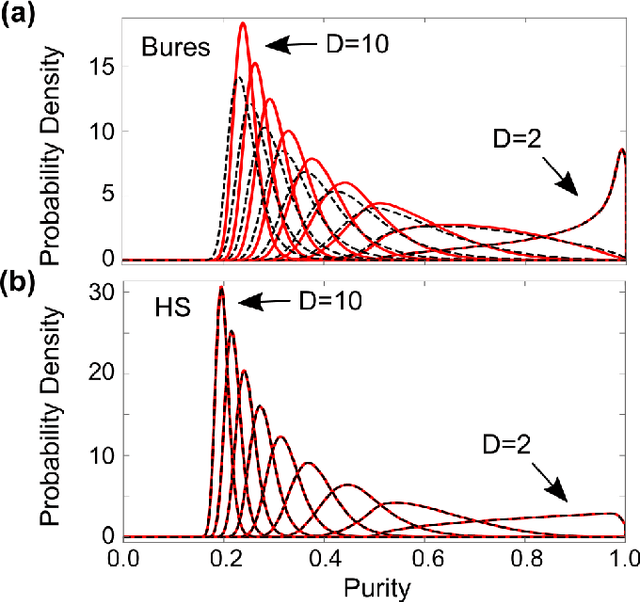
We consider the properties of a specific distribution of mixed quantum states of arbitrary dimension that can be biased towards a specific mean purity. In particular, we analyze mixtures of Haar-random pure states with Dirichlet-distributed coefficients. We analytically derive the concentration parameters required to match the mean purity of the Bures and Hilbert--Schmidt distributions in any dimension. Numerical simulations suggest that this value recovers the Hilbert--Schmidt distribution exactly, offering an alternative and intuitive physical interpretation for ensembles of Hilbert--Schmidt-distributed random quantum states. We then demonstrate how substituting these Dirichlet-weighted Haar mixtures in place of the Bures and Hilbert--Schmidt distributions results in measurable performance advantages in machine-learning-based quantum state tomography systems and Bayesian quantum state reconstruction. Finally, we experimentally characterize the distribution of quantum states generated by both a cloud-accessed IBM quantum computer and an in-house source of polarization-entangled photons. In each case, our method can more closely match the underlying distribution than either Bures or Hilbert--Schmidt distributed states for various experimental conditions.

On the experimental feasibility of quantum state reconstruction via machine learning

We determine the resource scaling of machine learning-based quantum state reconstruction methods, in terms of both inference and training, for systems of up to four qubits. Further, we examine system performance in the low-count regime, likely to be encountered in the tomography of high-dimensional systems. Finally, we implement our quantum state reconstruction method on a IBM Q quantum computer and confirm our results.

Machine learning assisted quantum state estimation

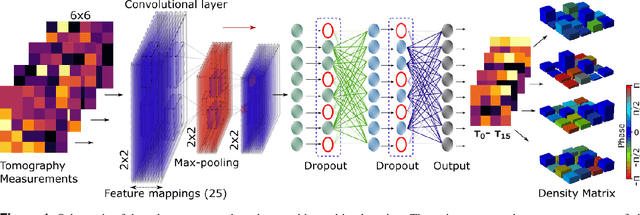
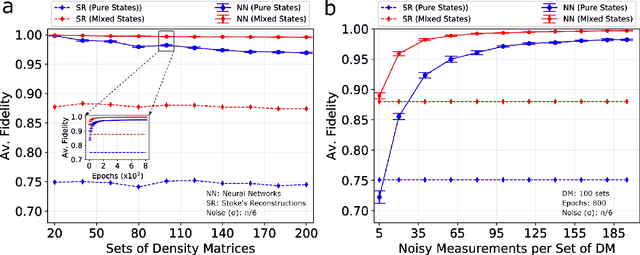
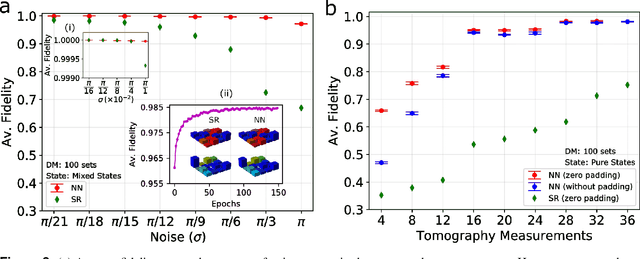
We build a general quantum state tomography framework that makes use of machine learning techniques to reconstruct quantum states from a given set of coincidence measurements. For a wide range of pure and mixed input states we demonstrate via simulations that our method produces functionally equivalent reconstructed states to that of traditional methods with the added benefit that expensive computations are front-loaded with our system. Further, by training our system with measurement results that include simulated noise sources we are able to demonstrate a significantly enhanced average fidelity when compared to typical reconstruction methods. These enhancements in average fidelity are also shown to persist when we consider state reconstruction from partial tomography data where several measurements are missing. We anticipate that the present results combining the fields of machine intelligence and quantum state estimation will greatly improve and speed up tomography-based quantum experiments.