Demonstration of machine-learning-enhanced Bayesian quantum state estimation

Machine learning (ML) has found broad applicability in quantum information science in topics as diverse as experimental design, state classification, and even studies on quantum foundations. Here, we experimentally realize an approach for defining custom prior distributions that are automatically tuned using ML for use with Bayesian quantum state estimation methods. Previously, researchers have looked to Bayesian quantum state tomography due to its unique advantages like natural uncertainty quantification, the return of reliable estimates under any measurement condition, and minimal mean-squared error. However, practical challenges related to long computation times and conceptual issues concerning how to incorporate prior knowledge most suitably can overshadow these benefits. Using both simulated and experimental measurement results, we demonstrate that ML-defined prior distributions reduce net convergence times and provide a natural way to incorporate both implicit and explicit information directly into the prior distribution. These results constitute a promising path toward practical implementations of Bayesian quantum state tomography.

Dimension-adaptive machine-learning-based quantum state reconstruction

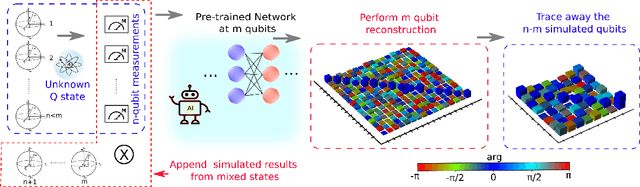
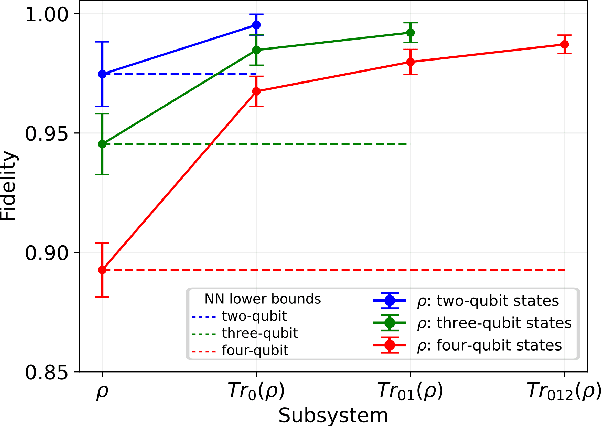
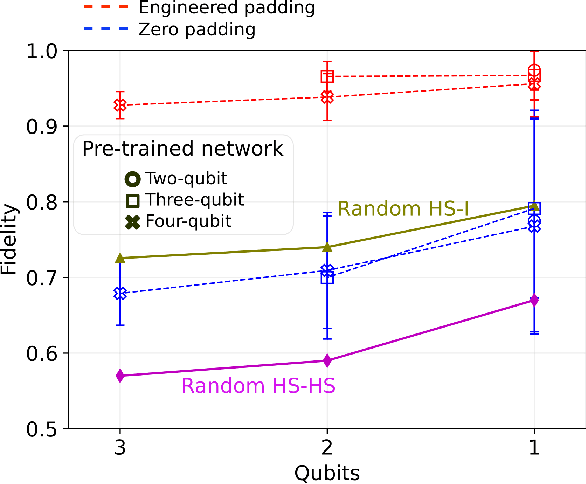
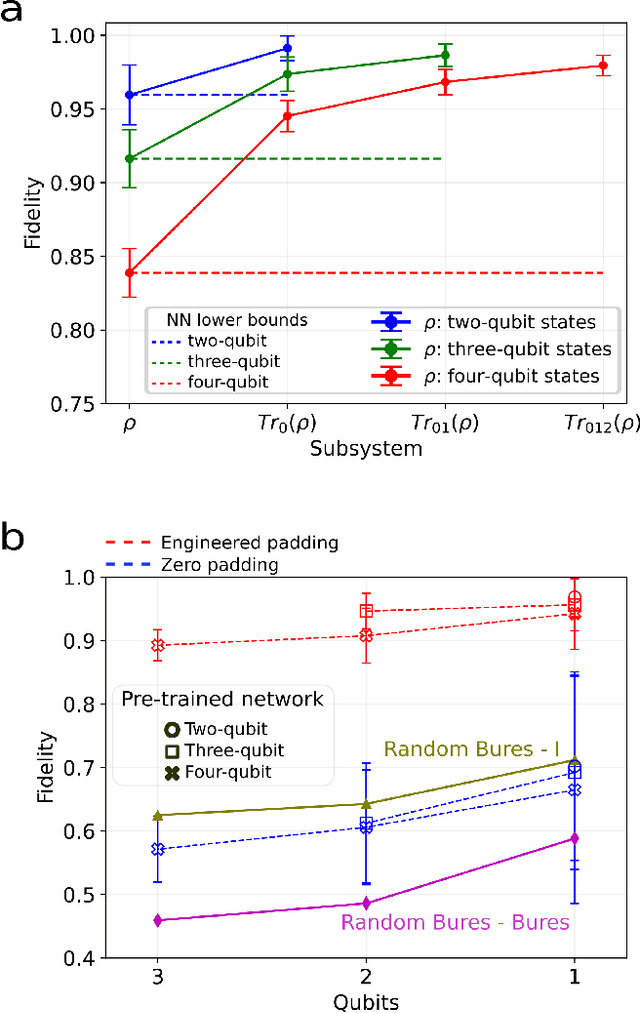
We introduce an approach for performing quantum state reconstruction on systems of $n$ qubits using a machine-learning-based reconstruction system trained exclusively on $m$ qubits, where $m\geq n$. This approach removes the necessity of exactly matching the dimensionality of a system under consideration with the dimension of a model used for training. We demonstrate our technique by performing quantum state reconstruction on randomly sampled systems of one, two, and three qubits using machine-learning-based methods trained exclusively on systems containing at least one additional qubit. The reconstruction time required for machine-learning-based methods scales significantly more favorably than the training time; hence this technique can offer an overall savings of resources by leveraging a single neural network for dimension-variable state reconstruction, obviating the need to train dedicated machine-learning systems for each Hilbert space.