Dimension-adaptive machine-learning-based quantum state reconstruction
Paper and Code
May 11, 2022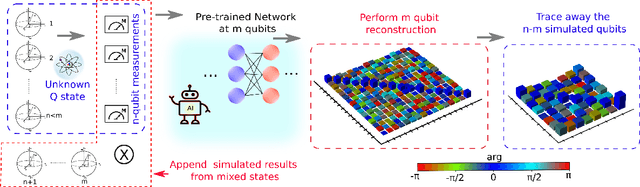
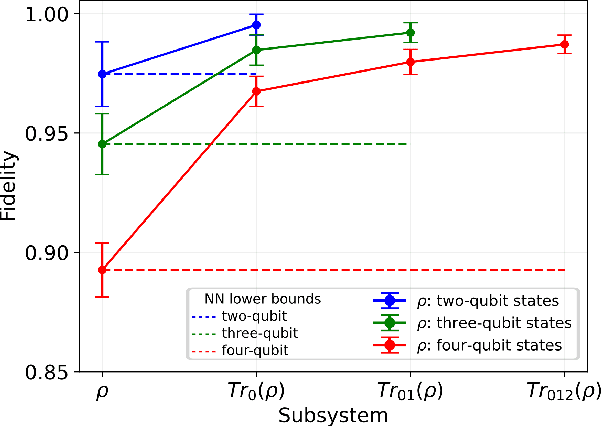
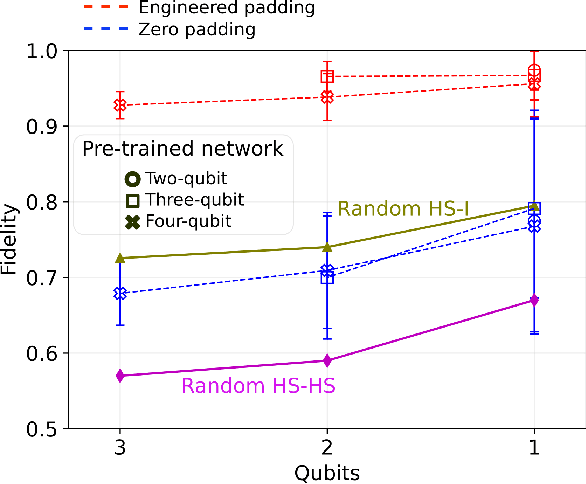
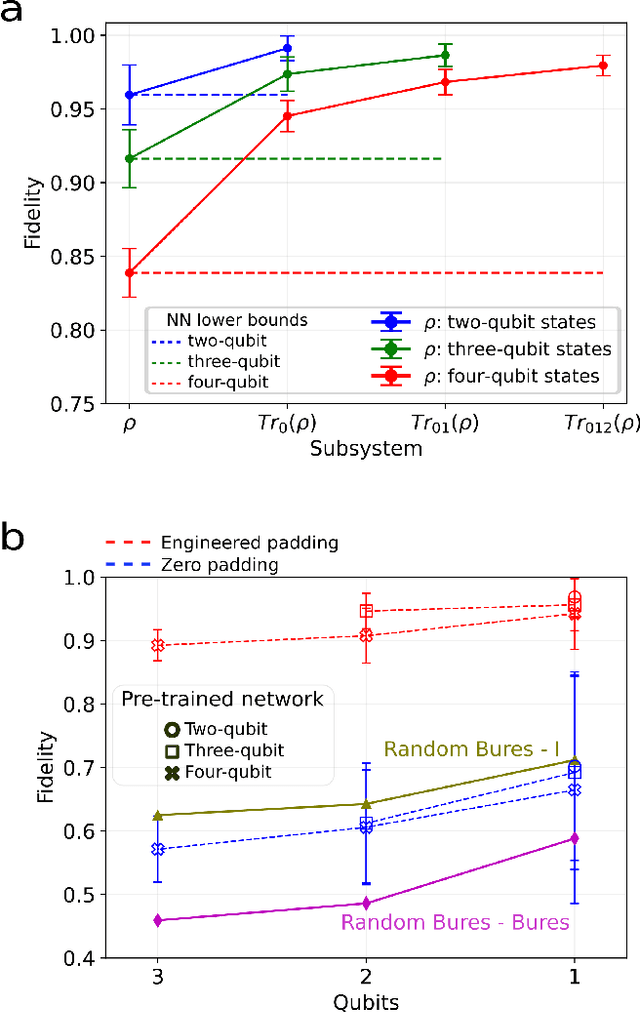
We introduce an approach for performing quantum state reconstruction on systems of $n$ qubits using a machine-learning-based reconstruction system trained exclusively on $m$ qubits, where $m\geq n$. This approach removes the necessity of exactly matching the dimensionality of a system under consideration with the dimension of a model used for training. We demonstrate our technique by performing quantum state reconstruction on randomly sampled systems of one, two, and three qubits using machine-learning-based methods trained exclusively on systems containing at least one additional qubit. The reconstruction time required for machine-learning-based methods scales significantly more favorably than the training time; hence this technique can offer an overall savings of resources by leveraging a single neural network for dimension-variable state reconstruction, obviating the need to train dedicated machine-learning systems for each Hilbert space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge