Curriculum reinforcement learning for quantum architecture search under hardware errors

The key challenge in the noisy intermediate-scale quantum era is finding useful circuits compatible with current device limitations. Variational quantum algorithms (VQAs) offer a potential solution by fixing the circuit architecture and optimizing individual gate parameters in an external loop. However, parameter optimization can become intractable, and the overall performance of the algorithm depends heavily on the initially chosen circuit architecture. Several quantum architecture search (QAS) algorithms have been developed to design useful circuit architectures automatically. In the case of parameter optimization alone, noise effects have been observed to dramatically influence the performance of the optimizer and final outcomes, which is a key line of study. However, the effects of noise on the architecture search, which could be just as critical, are poorly understood. This work addresses this gap by introducing a curriculum-based reinforcement learning QAS (CRLQAS) algorithm designed to tackle challenges in realistic VQA deployment. The algorithm incorporates (i) a 3D architecture encoding and restrictions on environment dynamics to explore the search space of possible circuits efficiently, (ii) an episode halting scheme to steer the agent to find shorter circuits, and (iii) a novel variant of simultaneous perturbation stochastic approximation as an optimizer for faster convergence. To facilitate studies, we developed an optimized simulator for our algorithm, significantly improving computational efficiency in simulating noisy quantum circuits by employing the Pauli-transfer matrix formalism in the Pauli-Liouville basis. Numerical experiments focusing on quantum chemistry tasks demonstrate that CRLQAS outperforms existing QAS algorithms across several metrics in both noiseless and noisy environments.

Enhancing variational quantum state diagonalization using reinforcement learning techniques

The development of variational quantum algorithms is crucial for the application of NISQ computers. Such algorithms require short quantum circuits, which are more amenable to implementation on near-term hardware, and many such methods have been developed. One of particular interest is the so-called the variational diagonalization method, which constitutes an important algorithmic subroutine, and it can be used directly for working with data encoded in quantum states. In particular, it can be applied to discern the features of quantum states, such as entanglement properties of a system, or in quantum machine learning algorithms. In this work, we tackle the problem of designing a very shallow quantum circuit, required in the quantum state diagonalization task, by utilizing reinforcement learning. To achieve this, we utilize a novel encoding method that can be used to tackle the problem of circuit depth optimization using a reinforcement learning approach. We demonstrate that our approach provides a solid approximation to the diagonalization task while using a small number of gates. The circuits proposed by the reinforcement learning methods are shallower than the standard variational quantum state diagonalization algorithm, and thus can be used in situations where the depth of quantum circuits is limited by the hardware capabilities.

Machine learning assisted quantum state estimation

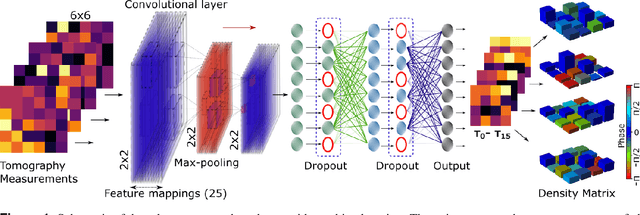
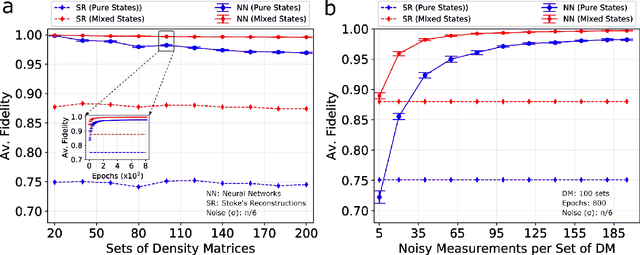
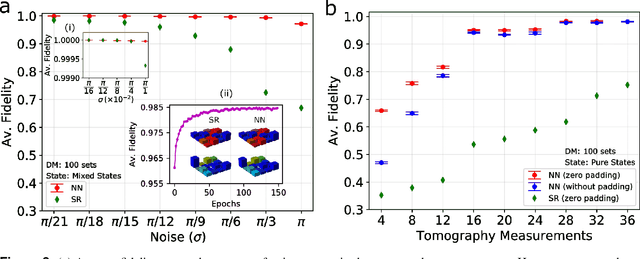
We build a general quantum state tomography framework that makes use of machine learning techniques to reconstruct quantum states from a given set of coincidence measurements. For a wide range of pure and mixed input states we demonstrate via simulations that our method produces functionally equivalent reconstructed states to that of traditional methods with the added benefit that expensive computations are front-loaded with our system. Further, by training our system with measurement results that include simulated noise sources we are able to demonstrate a significantly enhanced average fidelity when compared to typical reconstruction methods. These enhancements in average fidelity are also shown to persist when we consider state reconstruction from partial tomography data where several measurements are missing. We anticipate that the present results combining the fields of machine intelligence and quantum state estimation will greatly improve and speed up tomography-based quantum experiments.