Effective Ways to Build and Evaluate Individual Survival Distributions

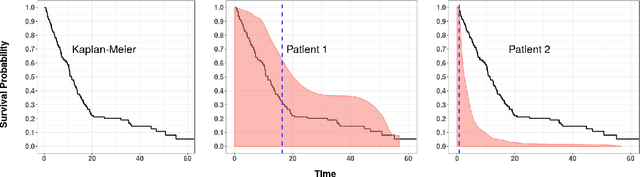
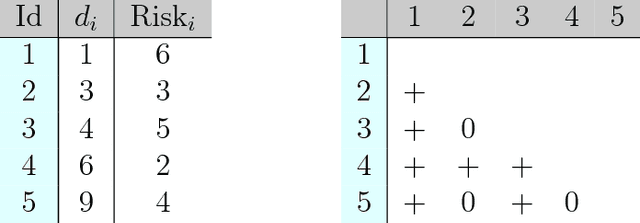
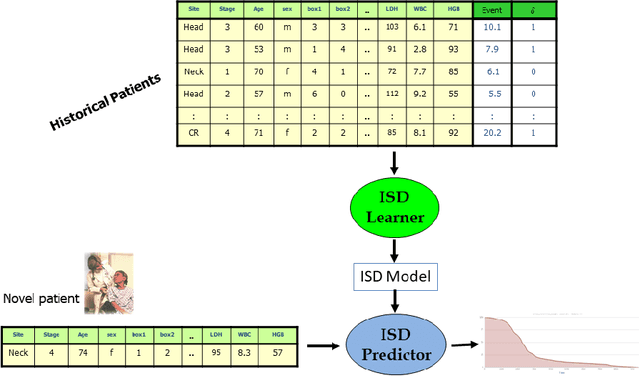
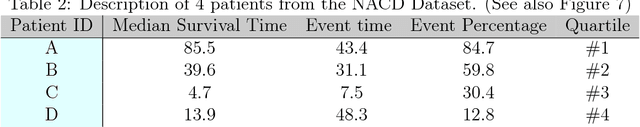
An accurate model of a patient's individual survival distribution can help determine the appropriate treatment for terminal patients. Unfortunately, risk scores (e.g., from Cox Proportional Hazard models) do not provide survival probabilities, single-time probability models (e.g., the Gail model, predicting 5 year probability) only provide for a single time point, and standard Kaplan-Meier survival curves provide only population averages for a large class of patients meaning they are not specific to individual patients. This motivates an alternative class of tools that can learn a model which provides an individual survival distribution which gives survival probabilities across all times - such as extensions to the Cox model, Accelerated Failure Time, an extension to Random Survival Forests, and Multi-Task Logistic Regression. This paper first motivates such "individual survival distribution" (ISD) models, and explains how they differ from standard models. It then discusses ways to evaluate such models - namely Concordance, 1-Calibration, Brier score, and various versions of L1-loss - and then motivates and defines a novel approach "D-Calibration", which determines whether a model's probability estimates are meaningful. We also discuss how these measures differ, and use them to evaluate several ISD prediction tools, over a range of survival datasets.

Improved Mean and Variance Approximations for Belief Net Responses via Network Doubling

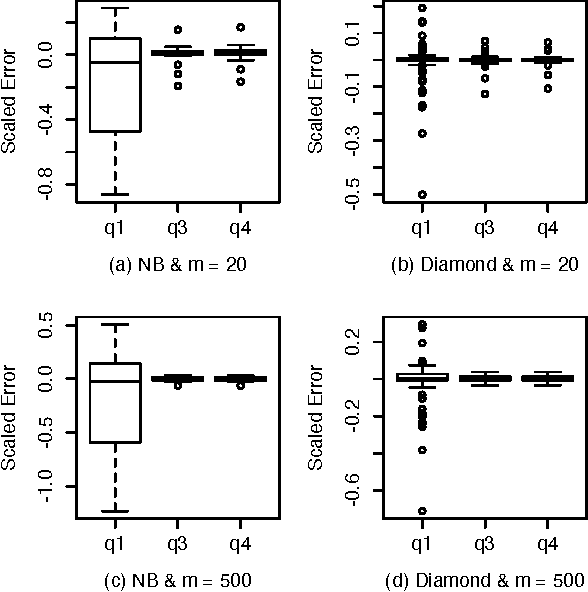
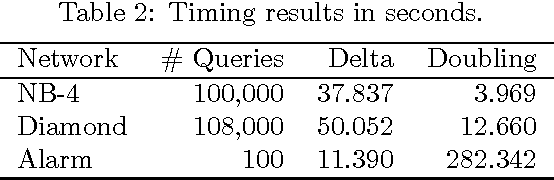
A Bayesian belief network models a joint distribution with an directed acyclic graph representing dependencies among variables and network parameters characterizing conditional distributions. The parameters are viewed as random variables to quantify uncertainty about their values. Belief nets are used to compute responses to queries; i.e., conditional probabilities of interest. A query is a function of the parameters, hence a random variable. Van Allen et al. (2001, 2008) showed how to quantify uncertainty about a query via a delta method approximation of its variance. We develop more accurate approximations for both query mean and variance. The key idea is to extend the query mean approximation to a "doubled network" involving two independent replicates. Our method assumes complete data and can be applied to discrete, continuous, and hybrid networks (provided discrete variables have only discrete parents). We analyze several improvements, and provide empirical studies to demonstrate their effectiveness.