Bayesian Error-Bars for Belief Net Inference

A Bayesian Belief Network (BN) is a model of a joint distribution over a setof n variables, with a DAG structure to represent the immediate dependenciesbetween the variables, and a set of parameters (aka CPTables) to represent thelocal conditional probabilities of a node, given each assignment to itsparents. In many situations, these parameters are themselves random variables - this may reflect the uncertainty of the domain expert, or may come from atraining sample used to estimate the parameter values. The distribution overthese "CPtable variables" induces a distribution over the response the BNwill return to any "What is Pr(H | E)?" query. This paper investigates thevariance of this response, showing first that it is asymptotically normal,then providing its mean and asymptotical variance. We then present aneffective general algorithm for computing this variance, which has the samecomplexity as simply computing the (mean value of) the response itself - ie,O(n 2^w), where n is the number of variables and w is the effective treewidth. Finally, we provide empirical evidence that this algorithm, whichincorporates assumptions and approximations, works effectively in practice,given only small samples.

Improved Mean and Variance Approximations for Belief Net Responses via Network Doubling

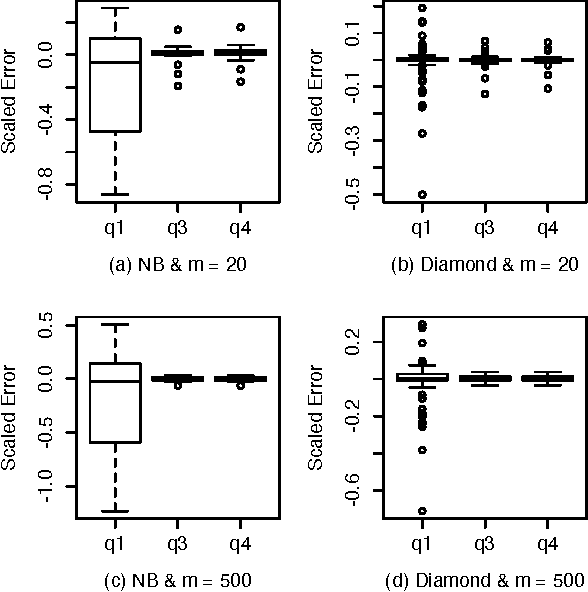
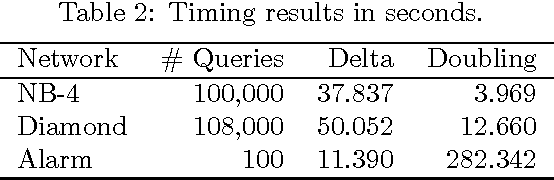
A Bayesian belief network models a joint distribution with an directed acyclic graph representing dependencies among variables and network parameters characterizing conditional distributions. The parameters are viewed as random variables to quantify uncertainty about their values. Belief nets are used to compute responses to queries; i.e., conditional probabilities of interest. A query is a function of the parameters, hence a random variable. Van Allen et al. (2001, 2008) showed how to quantify uncertainty about a query via a delta method approximation of its variance. We develop more accurate approximations for both query mean and variance. The key idea is to extend the query mean approximation to a "doubled network" involving two independent replicates. Our method assumes complete data and can be applied to discrete, continuous, and hybrid networks (provided discrete variables have only discrete parents). We analyze several improvements, and provide empirical studies to demonstrate their effectiveness.