Improved Mean and Variance Approximations for Belief Net Responses via Network Doubling
Paper and Code
May 09, 2012

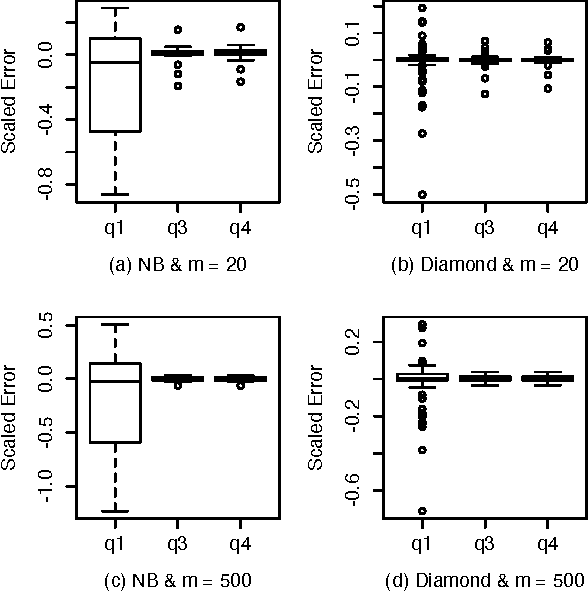
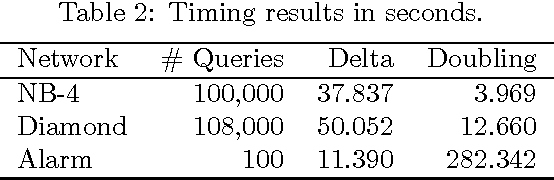
A Bayesian belief network models a joint distribution with an directed acyclic graph representing dependencies among variables and network parameters characterizing conditional distributions. The parameters are viewed as random variables to quantify uncertainty about their values. Belief nets are used to compute responses to queries; i.e., conditional probabilities of interest. A query is a function of the parameters, hence a random variable. Van Allen et al. (2001, 2008) showed how to quantify uncertainty about a query via a delta method approximation of its variance. We develop more accurate approximations for both query mean and variance. The key idea is to extend the query mean approximation to a "doubled network" involving two independent replicates. Our method assumes complete data and can be applied to discrete, continuous, and hybrid networks (provided discrete variables have only discrete parents). We analyze several improvements, and provide empirical studies to demonstrate their effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge