Effective Ways to Build and Evaluate Individual Survival Distributions
Paper and Code
Nov 28, 2018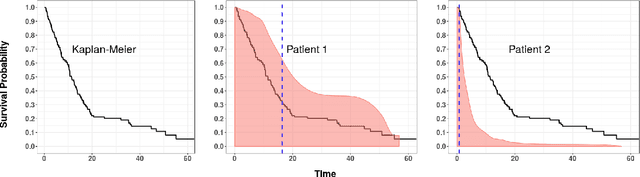
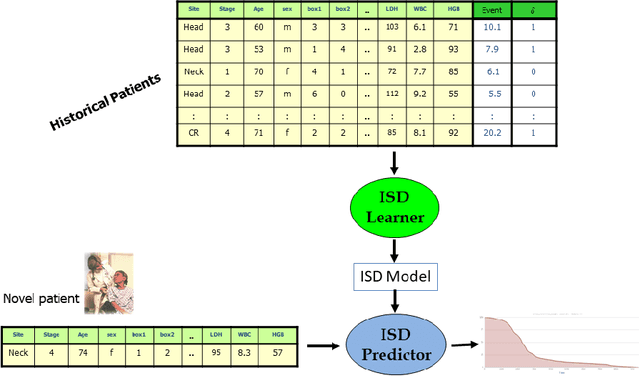
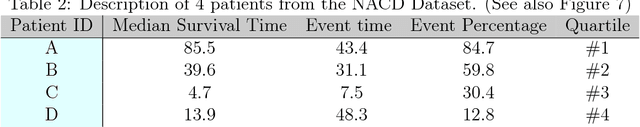
An accurate model of a patient's individual survival distribution can help determine the appropriate treatment for terminal patients. Unfortunately, risk scores (e.g., from Cox Proportional Hazard models) do not provide survival probabilities, single-time probability models (e.g., the Gail model, predicting 5 year probability) only provide for a single time point, and standard Kaplan-Meier survival curves provide only population averages for a large class of patients meaning they are not specific to individual patients. This motivates an alternative class of tools that can learn a model which provides an individual survival distribution which gives survival probabilities across all times - such as extensions to the Cox model, Accelerated Failure Time, an extension to Random Survival Forests, and Multi-Task Logistic Regression. This paper first motivates such "individual survival distribution" (ISD) models, and explains how they differ from standard models. It then discusses ways to evaluate such models - namely Concordance, 1-Calibration, Brier score, and various versions of L1-loss - and then motivates and defines a novel approach "D-Calibration", which determines whether a model's probability estimates are meaningful. We also discuss how these measures differ, and use them to evaluate several ISD prediction tools, over a range of survival datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge