Simultaneous Prediction Intervals for Patient-Specific Survival Curves

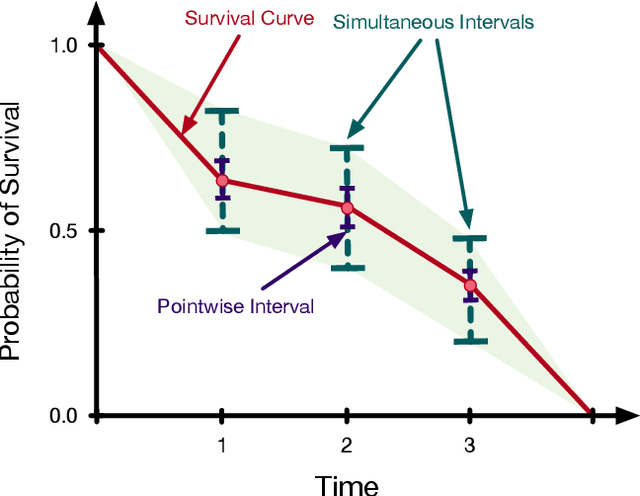
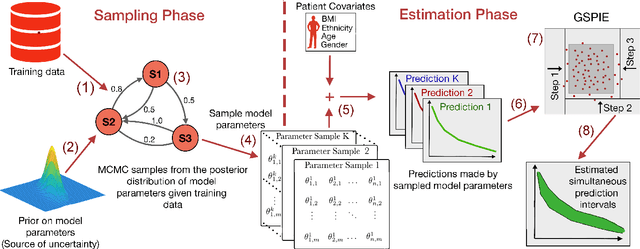
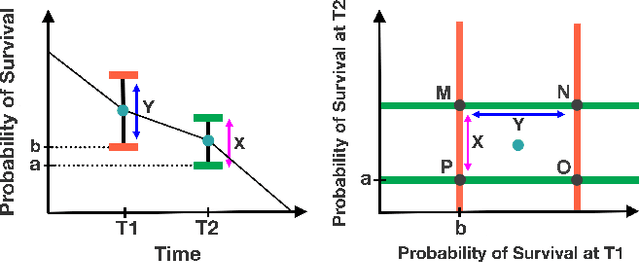
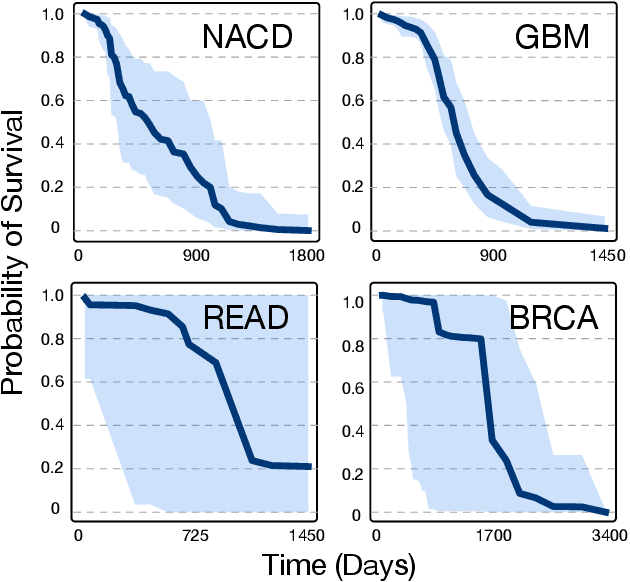
Accurate models of patient survival probabilities provide important information to clinicians prescribing care for life-threatening and terminal ailments. A recently developed class of models - known as individual survival distributions (ISDs) - produces patient-specific survival functions that offer greater descriptive power of patient outcomes than was previously possible. Unfortunately, at the time of writing, ISD models almost universally lack uncertainty quantification. In this paper, we demonstrate that an existing method for estimating simultaneous prediction intervals from samples can easily be adapted for patient-specific survival curve analysis and yields accurate results. Furthermore, we introduce both a modification to the existing method and a novel method for estimating simultaneous prediction intervals and show that they offer competitive performance. It is worth emphasizing that these methods are not limited to survival analysis and can be applied in any context in which sampling the distribution of interest is tractable. Code is available at https://github.com/ssokota/spie .

Effective Ways to Build and Evaluate Individual Survival Distributions

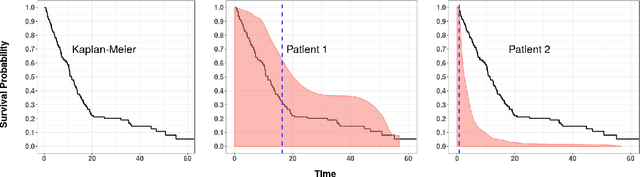
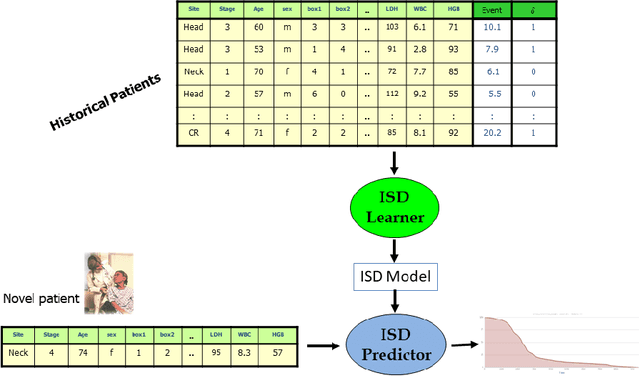
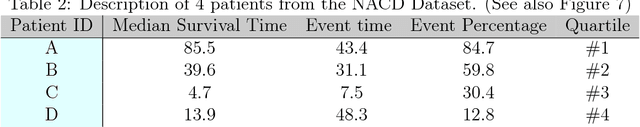
An accurate model of a patient's individual survival distribution can help determine the appropriate treatment for terminal patients. Unfortunately, risk scores (e.g., from Cox Proportional Hazard models) do not provide survival probabilities, single-time probability models (e.g., the Gail model, predicting 5 year probability) only provide for a single time point, and standard Kaplan-Meier survival curves provide only population averages for a large class of patients meaning they are not specific to individual patients. This motivates an alternative class of tools that can learn a model which provides an individual survival distribution which gives survival probabilities across all times - such as extensions to the Cox model, Accelerated Failure Time, an extension to Random Survival Forests, and Multi-Task Logistic Regression. This paper first motivates such "individual survival distribution" (ISD) models, and explains how they differ from standard models. It then discusses ways to evaluate such models - namely Concordance, 1-Calibration, Brier score, and various versions of L1-loss - and then motivates and defines a novel approach "D-Calibration", which determines whether a model's probability estimates are meaningful. We also discuss how these measures differ, and use them to evaluate several ISD prediction tools, over a range of survival datasets.