IterIS: Iterative Inference-Solving Alignment for LoRA Merging

Low-rank adaptations (LoRA) are widely used to fine-tune large models across various domains for specific downstream tasks. While task-specific LoRAs are often available, concerns about data privacy and intellectual property can restrict access to training data, limiting the acquisition of a multi-task model through gradient-based training. In response, LoRA merging presents an effective solution by combining multiple LoRAs into a unified adapter while maintaining data privacy. Prior works on LoRA merging primarily frame it as an optimization problem, yet these approaches face several limitations, including the rough assumption about input features utilized in optimization, massive sample requirements, and the unbalanced optimization objective. These limitations can significantly degrade performance. To address these, we propose a novel optimization-based method, named IterIS: 1) We formulate LoRA merging as an advanced optimization problem to mitigate the rough assumption. Additionally, we employ an iterative inference-solving framework in our algorithm. It can progressively refine the optimization objective for improved performance. 2) We introduce an efficient regularization term to reduce the need for massive sample requirements (requiring only 1-5% of the unlabeled samples compared to prior methods). 3) We utilize adaptive weights in the optimization objective to mitigate potential unbalances in LoRA merging process. Our method demonstrates significant improvements over multiple baselines and state-of-the-art methods in composing tasks for text-to-image diffusion, vision-language models, and large language models. Furthermore, our layer-wise algorithm can achieve convergence with minimal steps, ensuring efficiency in both memory and computation.

Stability and Sharper Risk Bounds with Convergence Rate $O(1/n^2)$

The sharpest known high probability excess risk bounds are up to $O\left( 1/n \right)$ for empirical risk minimization and projected gradient descent via algorithmic stability (Klochkov \& Zhivotovskiy, 2021). In this paper, we show that high probability excess risk bounds of order up to $O\left( 1/n^2 \right)$ are possible. We discuss how high probability excess risk bounds reach $O\left( 1/n^2 \right)$ under strongly convexity, smoothness and Lipschitz continuity assumptions for empirical risk minimization, projected gradient descent and stochastic gradient descent. Besides, to the best of our knowledge, our high probability results on the generalization gap measured by gradients for nonconvex problems are also the sharpest.

Towards Sharper Risk Bounds for Minimax Problems

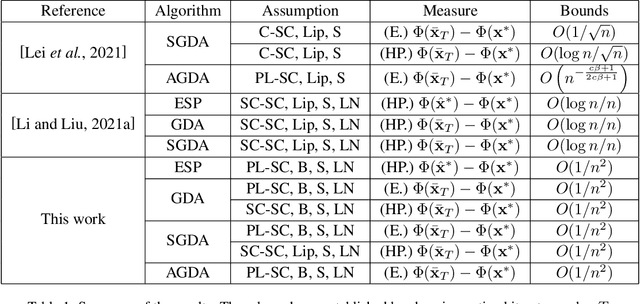
Minimax problems have achieved success in machine learning such as adversarial training, robust optimization, reinforcement learning. For theoretical analysis, current optimal excess risk bounds, which are composed by generalization error and optimization error, present 1/n-rates in strongly-convex-strongly-concave (SC-SC) settings. Existing studies mainly focus on minimax problems with specific algorithms for optimization error, with only a few studies on generalization performance, which limit better excess risk bounds. In this paper, we study the generalization bounds measured by the gradients of primal functions using uniform localized convergence. We obtain a sharper high probability generalization error bound for nonconvex-strongly-concave (NC-SC) stochastic minimax problems. Furthermore, we provide dimension-independent results under Polyak-Lojasiewicz condition for the outer layer. Based on our generalization error bound, we analyze some popular algorithms such as empirical saddle point (ESP), gradient descent ascent (GDA) and stochastic gradient descent ascent (SGDA). We derive better excess primal risk bounds with further reasonable assumptions, which, to the best of our knowledge, are n times faster than exist results in minimax problems.